Chapter Three. The Discrete Fourier Transform
Three The Discrete Fourier Transform
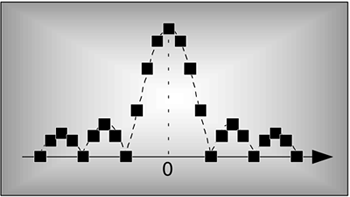
The discrete Fourier transform (DFT) is one of the two most common, and powerful, procedures encountered in the field of digital signal processing. (Digital filtering is the other.) The DFT enables us to analyze, manipulate, and synthesize signals in ways not possible with continuous (analog) signal processing. Even though it's now used in almost every field of engineering, we'll see applications for DFT continue to flourish as its utility becomes more widely understood. Because of this, a solid understanding of the DFT is mandatory for anyone working in the field of digital signal processing.
The DFT is a mathematical procedure used to determine the harmonic, or frequency, content of a discrete signal sequence. Although, for our purposes, a discrete signal sequence is a set of values obtained by periodic sampling of a continuous signal in the time domain, we'll find that the DFT is useful in analyzing any discrete sequence regardless of what that sequence actually represents. The DFT's origin, of course, is the continuous Fourier transform X(f) defined as

where x(t) is some continuous time-domain signal.[ ]
]
[
] Fourier is pronounced 'for-y
. In engineering school, we called Eq. (3-1) the "four-year" transform because it took about four years to do one homework problem.
In the field of continuous signal processing, Eq. (3-1) is used to transform an expression of a continuous time-domain function x(t) into a continuous frequency-domain function X(f). Subsequent evaluation of the X(f) expression enables us to determine the frequency content of any practical signal of interest and opens up a wide array of signal analysis and processing possibilities in the fields of engineering and physics. One could argue that the Fourier transform is the most dominant and widespread mathematical mechanism available for the analysis of physical systems. (A prominent quote from Lord Kelvin better states this sentiment: "Fourier's theorem is not only one of the most beautiful results of modern analysis, but it may be said to furnish an indispensable instrument in the treatment of nearly every recondite question in modern physics." By the way, the history of Fourier's original work in harmonic analysis, relating to the problem of heat conduction, is fascinating. References [1] and [2] are good places to start for those interested in the subject.)
With the advent of the digital computer, the efforts of early digital processing pioneers led to the development of the DFT defined as the discrete frequency-domain sequence X(m), where
Equation 3-2
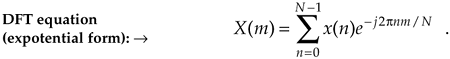
For our discussion of Eq. (3-2), x(n) is a discrete sequence of time-domain sampled values of the continuous variable x(t). The "e" in Eq. (3-2) is, of course, the base of natural logarithms and j = 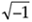 .
.
URL http://proquest.safaribooksonline.com/0131089897/ch03
 |
Amazon |  |
