FREQUENCY DEMODULATION ALGORITHMS
In Section 9.2 we discussed the notion of measuring the instantaneous frequency of a complex sinusoidal signal by computing the derivative of the signal's instantaneous q(n) phase as shown in Figure 13-60.
Figure 13-60. Frequency demodulator using an arctangent function.

This is the traditional discrete signal FM demodulation method, and it works fine. The demodulator's instantaneous output frequency is
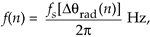
where fs is the sample rate in Hz.
Computing instantaneous phase q(n) requires an arctangent operation, which is difficult to implement accurately without considerable computational resources. Here's a scheme for computing Dq(n) for use in Eq. (13-111) without the intermediate q(n) phase computation (and its pesky arctangent)[53,54]. We derive the Dq(n) computation algorithm as follows, initially using continuous-time variables based on the following definitions:
Equation 13-112

First, we let r(t) = q(t)/i(t) be the signal for which we're trying to compute the derivative of its arctangent. The time derivative of tan–1[r(t)], a calculus identity, is
Equation 13-113
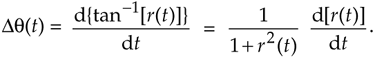
Because d[r(t)]/dt = d[q(t)/i(t)]/dt, we use the calculus identity for the derivative of a ratio to write
Equation 13-114
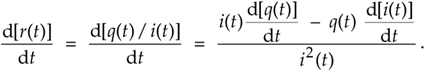
Plugging Eq. (13-114)'s result into Eq. (13-113), we have
Equation 13-115
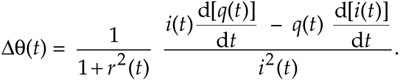
Replacing r(t) in Eq. (13-115) with q(t)/i(t) yields
Equation 13-116
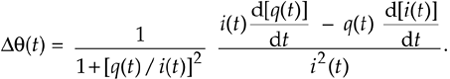
We're getting there. Next we multiply the numerator and denominator of the first ratio in Eq. (13-116) by i2(t), and replace t with our discrete time variable index n to arrive at our final result of
Equation 13-117
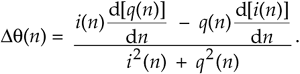
The implementation of this algorithm, where the derivatives of i(n) and q(n) are i'(n) and q'(n) respectively, is shown in Figure 13-61(a). The Df(n) output sequence is used in Eq. (13-111) to compute instantaneous frequency.
Figure 13-61. Frequency demodulator without arctangent: (a) standard process; (b) simplified process.
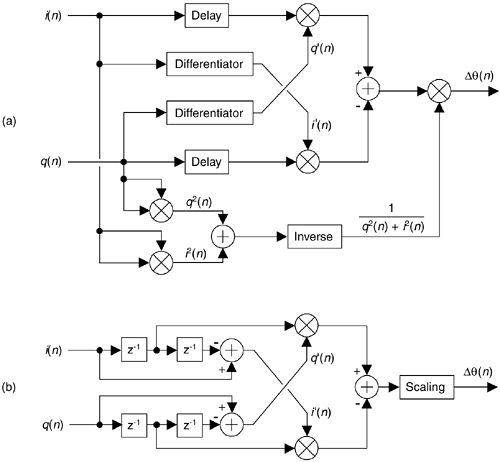
The Differentiator is an tapped-delay line FIR differentiating filter with an odd number of taps. Reference [54] reports acceptable results when the differentiator is a FIR filter having 1,0,–1 as coefficients. The Delay elements in Figure 13-61 are used to time-align i(n) and q(n) with the outputs of the differentiators such that the delay is (K–1)/2 samples when a K-tap differentiator is used. In practice, the Delay can be obtained by tapping off the center tap of the differentiating filter.
If the i(n)+jq(n) signal is purely FM and hard limited such that i2(n)+q2(n) = Constant, the denominator computations in Eq. (13-117) need not be performed. In this case, using the 1,0,–1 coefficient differentiators, the FM demodulator is simplified to that shown in Figure 13-61(b) where the Scaling operation is multiplication by the reciprocal of Constant.
URL http://proquest.safaribooksonline.com/0131089897/ch13lev1sec22
 |
Amazon |  |
