REPRESENTING REAL SIGNALS USING COMPLEX PHASORS | Chapter Eight. Quadrature Signals

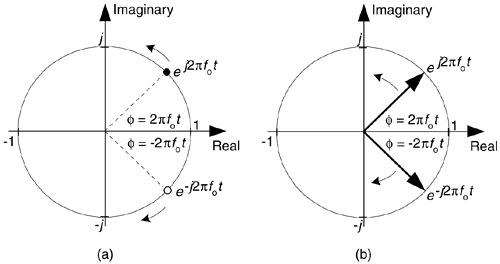
We now turn our attention to a complex number that is a function of time. Consider a number whose magnitude is one, and whose phase angle increases with time. That complex number is the 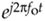point shown in Figure 8-5(a). (Here the 2pfo term is frequency in radians/second, and it corresponds to a frequency of fo cycles/second where fo is measured in hertz.) As time t gets larger, the complex number's phase angle increases and our number orbits the origin of the complex plane in a CCW direction. Figure 8-5(a) shows the number, represented by the solid dot, frozen at some arbitrary instant in time. If, say, the frequency fo = 2 Hz, then the dot would rotate around the circle two times per second. We can also think of another complex number 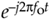(the white dot) orbiting in a clockwise direction because its phase angle gets more negative as time increases.

Figure 8-5. A snapshot, in time, of two complex numbers whose exponents change with time: (a) numbers shown as dots; (b) numbers shown as phasors.

Let's now call our two complex expressions, 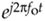and 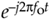, quadrature signals. They each have both real and imaginary parts, and they are both functions of time. Those 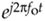and 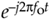expressions are often called complex exponentials in the literature.

We can also think of those two quadrature signals, 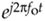and 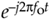, as the tips of two phasors rotating in opposite directions, as shown in Figure 8-5(b). We're going to stick with this phasor notation for now because it'll allow us to achieve our goal of representing real sinusoids in the context of the complex plane. Don't touch that dial!

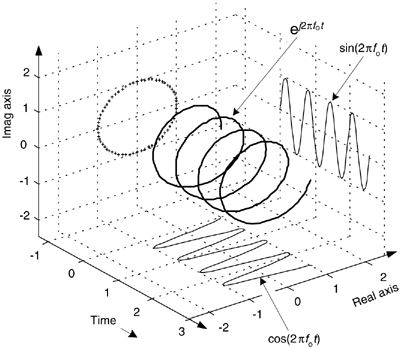
To ensure that we understand the behavior of a simple quadrature signal, Figure 8-6 shows the three-dimensional path of the 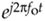signal as time passes. We've added the time axis, coming out of the page, to show how 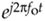follows a corkscrew path spiraling along, and centered about, the time axis. The real and imaginary parts of 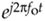are shown as the sine and cosine projections in Figure 8-6 and gives us additional insight into Eq. 8-7.

Figure 8-6. The motion of the 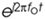complex signal as time increases.

To appreciate the physical meaning of our discussion here, let's remember that a continuous quadrature signal 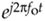= cos(2pfot) + jsin(2pfot) is not just mathematical mumbo jumbo. We can generate 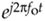in our laboratory and transmit it to another lab down the hall. All we need is two sinusoidal signal generators, set to the same frequency fo. (However, somehow we have to synchronize those two hardware generators so their relative phase shift is fixed at 90o.) Next we connect coax cables to the generators' output connectors and run those two cables, labeled cos for the cosine signal and sin for the sinewave signal, to their destination as shown in Figure 8-7.

Figure 8-7. Displaying a quadrature signal using an oscilloscope.

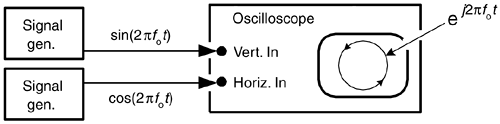
Now for a two-question pop quiz. First question: in the other lab, what would we see on the screen of an oscilloscope if the continuous real cos(2pfot) and sin(2pfot) signals were connected to the horizontal and vertical input channels, respectively, of the scope? (Remembering, of course, to set the scope's horizontal sweep control to the External position.) That's right. We'd see the scope's electron beam rotating counterclockwise around in a circle on the scope's screen.

Next, what would be seen on the scope's display if the cables were mislabeled and the two signals were inadvertently swapped? We'd see another circle, but this time it would be orbiting in a clockwise direction. This would be a neat little real-world demonstration if we set the signal generators' fo frequencies to, say, 1 Hz.

This oscilloscope example is meaningful and helps us answer the important question, "When we work with quadrature signals, how is the j-operator implemented in hardware?" The j-operator is implemented by how we treat the two signals relative to each other. We have to treat them orthogonally such that the real cos(2pfot) signal represents an east-west value, and the real sin(2pfot) signal represents an orthogonal north-south value. (By orthogonal, I mean the north-south direction is oriented exactly 90o relative to the east-west direction.) So in our oscilloscope example the j-operator is implemented merely by how the connections are made to the scope. The real cosine signal controls horizontal deflection and the real sine signal controls vertical deflection. The result is a two-dimensional quadrature signal represented by the instantaneous position of the dot on the scope's display. Our Figure 8-7 example reminds us of an important characteristic of quadrature signals: while real signals can be transmitted over a single cable, two cables are always necessary to transmit a quadrature (complex) signal.

Returning to Figure 8-5(b), ask yourself: "What's the vector sum of those two phasors as they rotate in opposite directions?" Think about this for a moment. That's right, the phasors' real parts will always add constructively, and their imaginary parts will always cancel. This means the summation of these 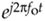and 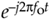phasors will always be a purely real number. Implementations of modern-day digital communications systems are based on this property!

To emphasize the importance of the real sum of these two complex sinusoids we'll draw yet another picture. Consider the waveform in the three-dimensional Figure 8-8 generated by the sum of two half-magnitude complex phasors, 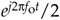and 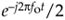, rotating in opposite directions about, and moving down along, the time axis.

Figure 8-8. A cosine represented by the sum of two rotating complex phasors.

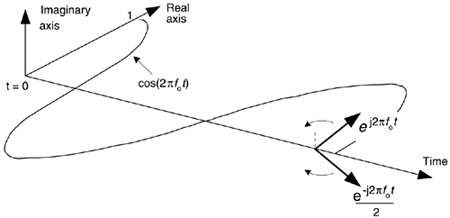
Thinking about these phasors, it's clear now why the cosine wave can be equated to the sum of two complex exponentials by

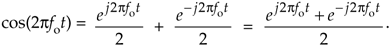
Eq. (8-13), a well known and important expression, is also called one of Euler's identities. We could have derived this identity by solving Eqs. (8-7) and (8-8) for jsin(ø), equating those two expressions, and solving that final equation for cos(ø). Similarly, we could go through the same algebra exercise and show a real sinewave as also the sum of two complex exponentials as

Equation 8-14

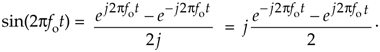
Look at Eqs. (8-13) and (8-14) carefully—they are the standard expressions for a cosine wave and a sinewave, using complex notation, and are seen throughout the literature of quadrature communications systems. To keep the reader's mind from spinning like those complex phasors, please realize that the sole purpose of Figures 8-5 through 8-8 is to validate the complex expressions of the cosine and sinewave given in Eqs. (8-13) and (8-11). Those two equations, along with Eqs. (8-7) and (8-8), are the Rosetta Stone of quadrature signal processing.[] We can now easily translate, back and forth, between real sinusoids and complex exponentials.

[] The Rosetta stone was a basalt slab found in Egypt in 1799. It had the same text written in three languages, two of them being Greek and Egyptian hieroglyphs. This enabled scholars to, finally, translate the ancient hieroglyphs.

Let's step back now and remind ourselves what we're doing. We are learning how real signals that can be transmitted down a coax cable, or digitized and stored in a computer's memory, can be represented in complex number notation. Yes, the constituent parts of a complex number are each real, but we're treating those parts in a special way—we're treating them in quadrature.

URL http://proquest.safaribooksonline.com/0131089897/ch08lev1sec3