A COMPLEX DOWN-CONVERSION EXAMPLE
We can use all we've learned so far about quadrature signals by exploring the process of quadrature-sampling. Quadrature sampling is the process of digitizing a continuous (analog) bandpass signal and down-converting its spectrum to be centered at zero Hz. Let's see how this popular process works by thinking of a continuous bandpass signal, of bandwidth B, centered about a carrier frequency of fc Hz as shown in Figure 8-17(a).
Figure 8-17. The "before and after" spectra of a quadrature-sampled signal.
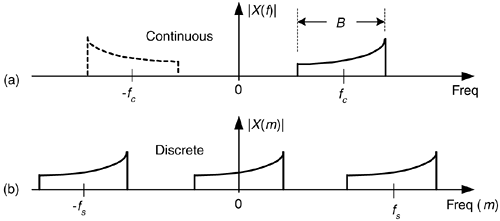
Our goal in quadrature sampling is to obtain a digitized version of the analog bandpass signal, but we want the digitized signal's discrete spectrum centered about zero Hz, not fc Hz as in Figure 8-17(b). That is, we want to mix a time signal with 
to perform complex down-conversion. The frequency fs is the digitizer's sampling rate in samples/second. We show replicated spectra in Figure 8-17(b) to remind ourselves of this effect when A/D conversion takes place.
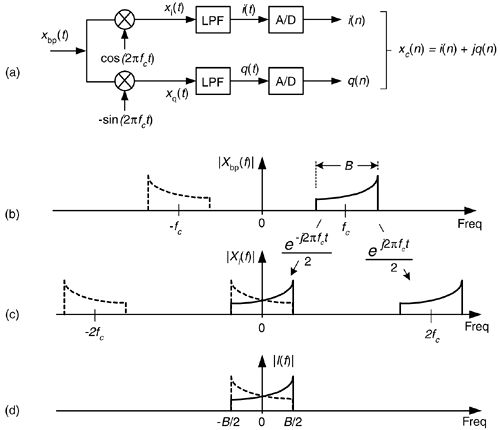
We can solve our sampling problem with the quadrature-sampling block diagram (also known as I/Q demodulation) shown in Figure 8-18(a). That arrangement of two sinusoidal oscillators, with their relative 90o phase, is often called a quadrature oscillator. First we'll investigate the in-phase (upper) path of the quadrature sampler. With the input analog xbp(t)'s spectrum shown in Figure 8-18(b), the spectral output of the top mixer is provided in Figure 8-18(c).
Figure 8-18. Quadrature-sampling: (a) block diagram; (b) input spectrum; (c) in-phase mixer output spectrum; (d) in-phase filter output spectrum.
Those 
and terms in Figure 8-18 remind us, from Eq. (8-13), that the constituent complex exponentials comprise a real cosine duplicate and translate each part of |Xbp(f)|'s spectrum to produce the |Xi(f)| spectrum. There is a magnitude loss of a factor of 2 in |Xi(f)|, but we're not concerned about that at this point. Figure 8-18(d) shows the output of the lowpass filter (LPF) in the in-phase path.
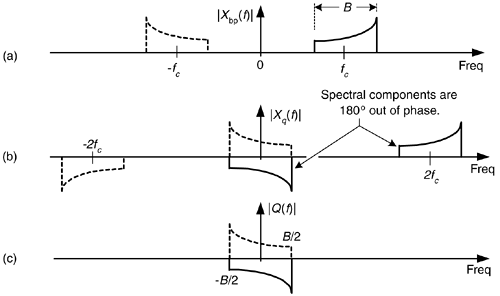
Likewise, Figure 8-19 shows how we get the filtered continuous quadrature phase portion (bottom path) of our desired complex signal by mixing xbp(t) with –sin(2pfct). From Eq. (8-14) we know that the complex exponentials comprising the real –sin(2pfct) sinewave are and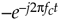 
. The minus sign in the 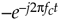term accounts for the down-converted spectra in |Xq(f)| being 180o out of phase with the up-converted spectra.
Figure 8-19. Spectra within the quadrature phase (lower) signal path of the block diagram.
This depiction of quadrature sampling can be enhanced if we look at the situation from a three-dimensional standpoint, as in Figure 8-20. There the +j factor rotates the "imaginary-only" Q(f) by 90o, making it "real-only." This jQ(f) is then added to I(f) to yield the spectrum of a complex continuous signal x(t) = i(t) + jq(t). Applying this signal to two A/D converters gives our final desired discrete time samples of xc(n) = i(n) + jq(n) in Figure 8-18(a) having the spectrum shown in Figure 8-17(b).
Figure 8-20. Three-dimensional view of combining the I(f) and Q(f) spectra to obtain the I(f) +jQ(f) spectra.
Some advantages of this quadrature-sampling scheme are:
- Each A/D converter operates at half the sampling rate of standard real-signal sampling.
- In many hardware implementations, operating at lower clock rates saves power.
- For a given fs sampling rate, we can capture wider band analog signals.
- Quadrature sequences make FFT processing more efficient due to a wider frequency range coverage.
- Quadrature sampling also makes it easier to measure the instantaneous magnitude and phase of a signal during demodulation.
- Knowing the instantaneous phase of signals enables coherent processing.
While the quadrature sampler in Figure 8-18(a) performed complex down-conversion, it's easy to implement complex up-conversion by merely conjugating the xc(n) sequence, effectively inverting xc(n)'s spectrum about zero Hz, as shown in Figure 8-21.
Figure 8-21. Using conjugation to control spectral orientation.
 |
Amazon |  |
