Section A.2. ARITHMETIC REPRESENTATION OF COMPLEX NUMBERS
A 2 ARITHMETIC REPRESENTATION OF COMPLEX NUMBERS
A complex number C is represented in a number of different ways in the literature, such as

Equation A-1'

Equation A-1''

Equation A-1'''
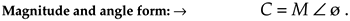
Equations (A-1'') and (A-1''') remind us that the complex number C can also be considered the tip of a phasor on the complex plane, with magnitude M, in the direction of ø degrees relative to the positive real axis as shown in Figure A-2. (We'll avoid calling phasor M a vector because the term vector means different things in different contexts. In linear algebra, vector is the term used to signify a one-dimensional matrix. On the other hand, in mechanical engineering and field theory, vectors are used to signify magnitudes and directions, but there are vector operations (scalar or dot product, and vector or cross-product) that don't apply to our definition of a phasor.) The relationships between the variables in this figure follow the standard trigonometry of right triangles. Keep in mind that C is a complex number, and the variables R, I, M, and ø are all real numbers. The magnitude of C, sometimes called the modulus of C, is
Equation A-2
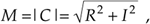
and, by definition, the phase angle, or argument, of C is the arctangent of I/R, or
Equation A-3

The variable ø in Eq. (A-3) is a general angle term. It can have dimensions of degrees or radians. Of course, we can convert back and forth between degrees and radians using p radians = 180°. So, if ør is in radians and ød is in degrees, then we can convert ør to degrees by the expression
Equation A-4
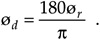
Likewise, we can convert ød to radians by the expression
Equation A-5

The exponential form of a complex number has an interesting characteristic that we need to keep in mind. Whereas only a single expression in rectangular form can describe a single complex number, an infinite number of exponential expressions can describe a single complex number; that is, while, in the exponential form, a complex number C can be represented by C = Mejø, it can also be represented by
Equation A-6

where n = ±1, ±2, ±3, . . . and ø is in radians. When ø is in degrees, Eq. (A-6) is in the form
Equation A-7
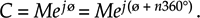
Equations (A-6) and (A-7) are almost self-explanatory. They indicate that the point on the complex plane represented by the tip of the phasor C remains unchanged if we rotate the phasor some integral multiple of 2p radians or an integral multiple of 360°. So, for example, if C = Mej(20°), then
Equation A-8

The variable ø, the angle of the phasor in Figure A-2, need not be constant. We'll often encounter expressions containing a complex sinusoid that takes the form
Equation A-9
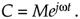
Equation (A-9) represents a phasor of magnitude M whose angle in Figure A-2 is increasing linearly with time at a rate of w radians each second. If w = 2p, the phasor described by Eq. (A-9) is rotating counterclockwise at a rate of 2p radians per second—one revolution per second—and that's why w is called the radian frequency. In terms of frequency, Eq. (A-9)'s phasor is rotating counterclockwise at w = 2pf radians per second, where f is the cyclic frequency in cycles per second (Hz). If the cyclic frequency is f = 10 Hz, the phasor is rotating 20p radians per second. Likewise, the expression
Equation A-9'
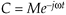
represents a phasor of magnitude M that rotates in a clockwise direction about the origin of the complex plane at a negative radian frequency of –w radians per second.
URL http://proquest.safaribooksonline.com/0131089897/app01lev1sec2
 |
Amazon |  |
