FAST MULTIPLICATION OF COMPLEX NUMBERS
The multiplication of two complex numbers is one of the most common functions performed in digital signal processing. It's mandatory in all discrete and fast Fourier transformation algorithms, necessary for graphics transformations, and used in processing digital communications signals. Be it in hardware or software, it's always to our benefit to streamline the processing necessary to perform a complex multiply whenever we can. If the available hardware can perform three additions faster than a single multiplication, there's a way to speed up a complex multiply operation [16].
The multiplication of two complex numbers, a + jb and c + jd, results in the complex product
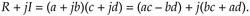
We can see that Eq. (13-14) requires four multiplications and two additions. (From a computational standpoint we'll assume a subtraction is equivalent to an addition.) Instead of using Eq. (13-14), we can calculate the following intermediate values
Equation 13-15
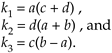
We then perform the following operations to get the final R and I
Equation 13-16
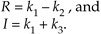
The reader is invited to plug the k values from Eq. (13-15) into Eq. (13-16) to verify that the expressions in Eq. (13-16) are equivalent to Eq. (13-14). The intermediate values in Eq. (13-15) required three additions and three multiplications, while the results in Eq. (13-16) required two more additions. So we traded one of the multiplications required in Eq. (13-14) for three addition operations needed by Eq. (13-15) and Eq. (13-16). If our hardware uses fewer clock cycles to perform three additions than a single multiplication, we may well gain overall processing speed by using Eq. (13-15) and Eq. (13-16) instead of Eq. (13-14) for complex multiplication.
URL http://proquest.safaribooksonline.com/0131089897/ch13lev1sec4
 |
Amazon |  |
