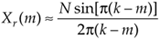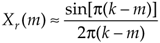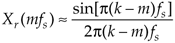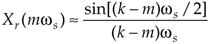THE DFT SINGLE-BIN FREQUENCY RESPONSE TO A REAL COSINE INPUT
Now that we understand the DFT's overall N-point (or N-bin) frequency response to a real cosine of k cycles per sample interval, we conclude this chapter by determining the frequency response of a single DFT bin. We can think of a single DFT bin as a kind of bandpass filter, and this useful notion is used, for example, to describe DFT scalloping loss (Section 3.10), employed in the design of frequency-domain filter banks, and applied in a telephone frequency multiplexing technique known as transmultiplexing[15]. To determine a DFT single-bin's frequency response, consider applying a real xr(n) cosine sequence to a DFT and monitoring the output magnitude of just the m = k bin. Let's say the initial frequency of the input cosine sequence starts at a frequency of k<m cycles and increases up to a frequency of k>m cycles in the sample interval. If we measure the DFT's m = k bin during that frequency sweep, we'll see that its output magnitude must track the input cosine sequence's continuous spectrum, shown as the shaded curves in Figure 3-45.
Figure 3-45. Determining the output magnitude of the mth bin of an N-point DFT: (a) when the real xr(n) has k = m–2.5 cycles in the time sequence; (b) when the real xr(n) has k = m–1.5 cycles in the time sequence; (c) when the real xr(n) has k = m cycles in the time sequence; (d) the DFT single-bin frequency magnitude response of the m = k bin.
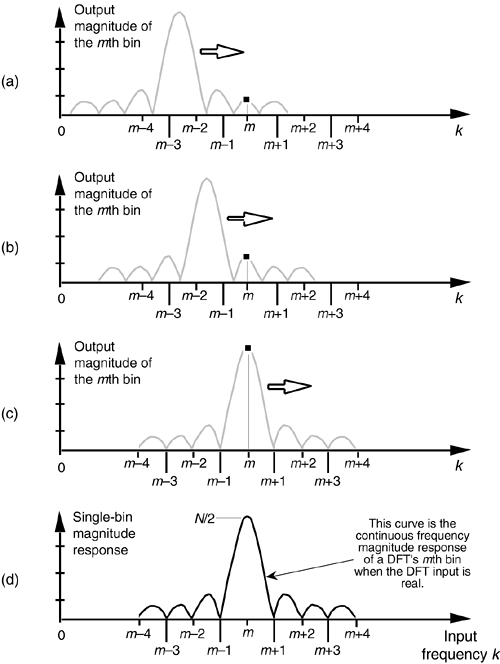
Table 3-4. Various Forms of the Positive Frequency Amplitude Response of the DFT to a Real Cosine Input Having k Cycles in the Sample Interval
|
Description |
Expression |
|---|---|
|
Real input DFT amplitude response in terms of the integral frequency variable m [From Eq. (3-73)] |
|
|
Alternate form of the real input DFT amplitude response in terms of the integral frequency variable m [based on Eq. (3-49)] |
Equation 3-75
|
|
Amplitude normalized real input DFT response in terms of the integral frequency variable m |
Equation 3-76
|
|
Real input DFT response in terms of the sample rate fs in Hz |
Equation 3-77
|
|
Amplitude normalized real input DFT response in terms of the sample rate fs in Hz |
Equation 3-78
|
|
Amplitude normalized real input DFT response in terms of the sample rate ws in radians/s |
Equation 3-79
|
Figure 3-45(a) shows the m = k bin's output when the input xr(n)'s frequency is k = m–2.5 cycles per sample interval. Increasing xr(n)'s frequency to k = m–1.5 cycles per sample interval results in the m = k bin's output, shown in Figure 3-45(b). Continuing to sweep xr(n)'s frequency higher, Figure 3-45(c) shows the m = k bin's output when the input frequency is k = m. Throughout our input frequency sweeping exercise, we can see that the m = k bin's output magnitude must trace out the cosine sequence's continuous spectrum, shown by the solid curve in Figure 3-45(d). This means that a DFT's single-bin frequency magnitude response, to a real input sinusoid, is that solid sinc function curve defined by Eqs. (3-74) through (3-79).
URL http://proquest.safaribooksonline.com/0131089897/ch03lev1sec16
 |
Amazon |  |