RF Propagation with 802.11

In fixed networks, signals are confined to wire pathways, so network engineers do not need to know anything about the physics of electrical signal propagation. Instead, there are a few rules used to calculate maximum cable length, and as long as the rules are obeyed, problems are rare. RF propagation is not anywhere near as simple.

Signal Reception and Performance

Space is full of random electromagnetic waves, which can easily be heard by tuning a radio to an unused frequency. Radio communication depends on making a signal intelligible over the background noise. As conditions for reception degrade, the signal gets closer to the noise floor. Performance is determined largely by the the most important factor, the signal-to-noise ratio (SNR). In Figure 10-2, the SNR is illustrated by the height of the peak of the signal above the noise floor.

Figure 10-2. Signal-to-noise ratio and the noise floor

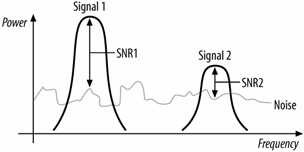
Having a strong signal is important, but not the whole story. Strong signals can be hard to pick out of noisy environments. In some situations, it may be possible to raise the power to compensate for a high noise floor. Unlicensed networks have only limited ability to raise power because of tight regulatory constraints. As a result, more effort is placed on introducing as little additional noise as possible before attempting to decode the radio signal.

The Shannon limit

Interestingly enough, there is no theoretical maximum to the amount of data that can be carried by a radio channel. The capacity of a communications channel is given by the Shannon-Hartley theorem, which was proved by Bell Labs researcher Claude Shannon in 1948. The theorem expresses the mathematical limit of the capacity of a communications channel, which is named after the theorem and is often called the Shannon limit or the Shannon capacity. The original Shannon theorem expressed the maximum capacity C bits per second as a function of the bandwidth W in Hertz, and the absolute ratio of signal power to noise. If the gain is measured in decibels, simply solve the equation that defines a decibel for the power ratio for the second form.

Figure 10-3 shows the Shannon limit as a function of the signal-to-noise ratio. Shannon's theorem reflects a theoretical reality of an unlimited bit rate. To get to an unlimited bit rate, the code designer can require an arbitrarily large number of signal levels to distinguish between bits, but the fine distinctions between the arbitrarily close signal rates will be swamped by the noise. One of the major goals for 802.11 PHY designers is to design encoding rates as close to the Shannon limit as possible.

Alternatively, the Shannon theorem can be used to prescribe the minimum theoretical signal to noise ratio to attain a given data rate. Solve the previous equations for the signal to noise ratio:

S/N = 2 ^ (C/W) - 1 (S/N as power ratio)

SNR = 10 * log10 (2 ^ (C/W) - 1) (SNR as dB)

Figure 10-3. Shannon limit as a function of SNR

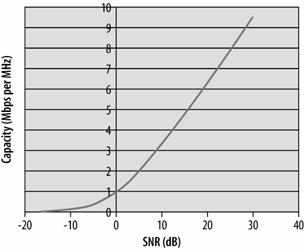
Take 802.11a as an example. A single 20 MHz channel can carry a signal at a data rate up to 54 Mbps. Solving for the required signal-to-noise ratio yields 7.4 dB, which is much lower than what is required by most real products on the market, reflecting the need of products to work in the real-world with much worse than ideal performance.[*]

[*] Or, as another example, the telephone network makes channels with a frequency band of 180 Hz to 3.2 kHz, at a signal-to-noise ratio of 45 dB. That makes the maximum theoretical speed of an analog signal about 45 kbps. The trick behind the 56 kbps modem is that the downstream path is all digital, and as a result has a higher signal-to-noise ratio.

Decibels and Signal Strength

Amplifiers may boost signals by orders of magnitude. Rather than keep track of all those zeroes, amplifier power is measured in decibels (dB).

dB = 10 x log10 (power out/power in)

Decibel ratings are positive when the output is larger than the input and negative when the output is smaller than the input. Each 10-dB change corresponds to a factor of 10, and 3-dB changes are a factor of 2. Thus, a 33-dB change corresponds to a factor of 2000:

33 dB = 10 dB + 10 dB + 10 dB + 3 dB = 10 x 10 x 10 x 2 = 2000

Power is sometimes measured in dBm, which stands for dB above one milliwatt. To find the dBm ratio, simply use 1 mW as the input power in the first equation.

It is helpful to remember that doubling the power is a 3-dB increase. A 1-dB increase is roughly equivalent to a power increase of 25%. With these numbers in mind, you can quickly perform most gain calculations in your head.

 

Path Loss, Range, and Throughput

In 802.11, the speed of the network depends on range. Several modulation types are defined by the various 802.11 standards, ranging in speed from 1 Mbps to 54 Mbps. Receiver circuits must distinguish between states to extract bits from radio waves. Higher speed modulations pack more bits into a given time interval, and require a cleaner signal (and thus higher signal-to-noise ratio) to successfully decode.

As radio signals travel through space, they degrade. For the most part, the noise floor will be relatively constant over the limited range of an 802.11 network. Over distance, the degradation of the signal will limit the signal-to-noise ratio at the receiver. As a station strays farther from an access point, the signal level drops; with a constant noise floor, the degraded signal will result in a degraded signal to noise ratio. Figure 10-4 illustrates this concept. As range from the access point increases, the received signal gets closer to the noise floor. Stations that are closer have higher signal to noise ratios. As a matter of network engineering, when the signal-to-noise ratio gets too small to support a high data rate, the station will fall back to a lower data rate with less demanding signal-to-noise ratio requirements.

Figure 10-4. Throughput versus distance

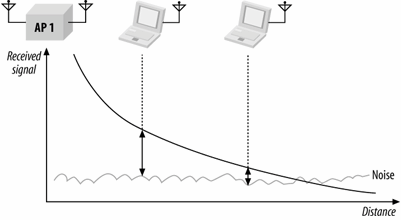
When there are no obstacles to obstruct the radio wave, the signal degradation can be calculated with the following equation. The loss in free-space is sometimes called the path loss because it is the minimum loss that would be expected along a path with a given length. Path loss depends on the distance and the frequency of the radio wave. Higher distances and higher frequencies lead to higher path loss. One reason why 802.11a has shorter range than 802.11b and 802.11g is that the path loss is much higher at the 5 GHz used by 802.11a. The equation for free-space path loss is:

Path loss (dB) = 32.5 + 20 log F + log d

where the frequency F is expressed in GHz, and the distance d is expressed in meters. Path loss is not, however, the only determinant of range. Obstacles such as walls and windows will reduce the signal, and antennas and amplifiers may be used to boost the signal, which compensates for transmission losses. Range calculations often include a fudge factor called the link margin to account for unforeseen losses.

Total loss = TX power + TX antenna gain - path loss - obstacle loss - link margin + RX antenna gain

Multipath Interference

Although there is a relatively simple equation for predicting radio propagation, it is only an estimate for 802.11 networks. In addition to straight-line path losses, there are other phenomena that can inhibit signal reception with 802.11. One of the major problems that plague radio networks is multipath fading. Waves are added by superposition. When multiple waves converge on a point, the total wave is simply the sum of any component waves. Figure 10-5 shows a few examples of superposition.

Figure 10-5. Wave combination by superposition

In Figure 10-5 (c), the two waves are almost exactly the opposite of each other, so the net result is almost nothing. Unfortunately, this result is more common than you might expect in wireless networks. Most 802.11 equipment uses omnidirectional antennas, so RF energy is radiated in every direction. Waves spread outward from the transmitting antenna in all directions and are reflected by surfaces in the area. Figure 10-6 shows a highly simplified example of two stations in a rectangular area with no obstructions.

Figure 10-6. Multiple paths

This figure shows three paths from the transmitter to the receiver. The wave at the receiver is the sum of all the different components. It is certainly possible that the paths shown in Figure 10-6 will all combine to give a net wave of 0, in which case the receiver will not understand the transmission because there is no transmission to be received.

Because the interference is a delayed copy of the same transmission on a different path, the phenomenon is called multipath fading or multipath interference. In many cases, multipath interference can be resolved by changing the orientation or position of the receiver.

Inter-Symbol Interference (ISI)

Multipath fading is a special case of inter-symbol interference. Waves that take different paths from the transmitter to the receiver will travel different distances and be delayed with respect to each other, as in Figure 10-7. Once again, the two waves combine by superposition, but the effect is that the total waveform is garbled. In real-world situations, wavefronts from multiple paths may be added. The time between the arrival of the first wavefront and the last multipath echo is called the delay spread. Longer delay spreads require more conservative coding mechanisms. 802.11b networks can handle delay spreads of up to 500 ns, but performance is much better when the delay spread is lower. When the delay spread is large, many cards will reduce the transmission rate; several vendors claim that a 65-ns delay spread is required for full-speed 11-Mbps performance at a reasonable frame error rate. (Discussion of reading the specification sheets is found in Chapter 16.) Analysis tools can be used to measure the delay spread.

Figure 10-7. Inter-symbol interference