Data Connection Resources

Data Connection Resources (DCRs) are new in Domino 6. They permit DECS to be extended directly into Domino forms. There are four major areas that must be set up to implement DCRs:

• Database properties
• Data connections (under Shared Resources)
• Form properties
• Field properties

Database Properties

A new option on the database properties dialog box is the Allow Connections to External Databases Using DCRs selection. It's off by default, but it must be on for the DCRs to function properly (see Figure 22.21).

Figure 22.21. To utilize DCRs, the Allow Connections to External Databases Using DCRs option must be checked.

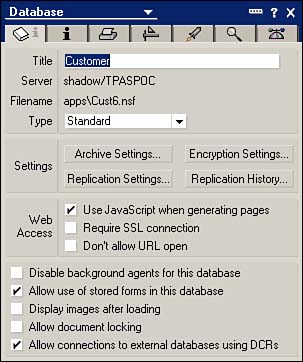
Leave this option off until you're done with the development and test of your DCRs. However, you must turn this option off if you need to initialize the keys of the database.

Turning DCR Connections On and Off

Just turning the Allow Connections to External Databases Using DCRs on and off does not necessarily take effect immediately. It takes effect only after the database has been opened and closed. When you change the check box for the first time, a dialog box emerges to remind you of that fact. You have the option to always be reminded or to turn off this reminder.

Data Connections

To allow a form to connect to an external database, a connection must be defined. Before DCRs, this could be defined only in DECS (or LEI). Now, however, the connection definition has been moved directly into the database under Shared Resources (see Figure 22.22).

Figure 22.22. Data Connections ”a new item under Shared Resources in Domino 6.

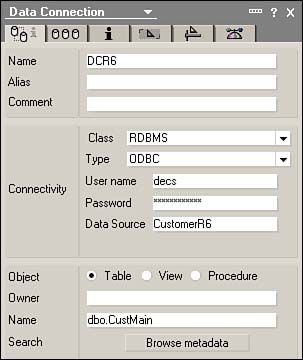
Data connections (DCs) define the method of connectivity between the database and external databases. A DC is defined by its name and alias, and then its connectivity information, and finally the connectivity details.

Defining a name for the DC is fairly straightforward ”just like all other design elements in Domino. However, the connectivity information is a little more complex. Here you must specify the following:

• Class
• Type
• Username
• Password
• Data Source

The class is the type of external database system you're accessing. Currently, RDBMS is the only option, but that's sure to change.

Type defines what type of connection. This is the same as choosing the type of connection in DECS and offers similar built-in options: DB2, Oracle, Oracle8, Sybase, ODBC, and OLEDB.

Username and password are just what you expect; in this case, they're for accessing the database system. There isn't an option to encrypt them as there is in DECS, but we haven't found where Notes stores these settings, so they might be secure.

The last item is the data source, which is the name of the data source from the perspective of the Domino server. So, just like in DECS, you must make sure that the connectivity software for the external system you plan to use is available to the Domino server that will host this application.

The last section on the first tab of the DCR definition is the connectivity details. Here you define the following:

• Object
• Owner
• Name
• For Procedures, Open , Update , Create , Delete Events

For tables and views, there's a Browse Metadata button at the bottom that enables you to pick from a list the external database element that you would like this DCR to represent. Procedures have a folder icon next to each event ( Open , Update , Create , Delete ), which enables you to pick the stored procedure from the external system. (Most RDBMSs call these stored procedures; however, there a few that refer to these procedures as functions. )

The next item is to enter the owner of the element type that you selected under Object. Many RDBMSs support the idea of schemas and, therefore, they also support the idea of objects with the same names but having different owners to distinguish them. Some RDBMSs do not, or they do not enforce the required owner field.

The Name field is the actual name of the object in the external system. This can be typed in by hand, or can be picked by the Browse Metadata button for tables and views and by the folder icon for each event for procedures.

Events in DCRs Are Not the Same as in DECS

For some reason, specifying the events on which the system is to fire the connection is reserved exclusively for procedures. Tables and views assume that you're supporting Open , Update , Create , and Delete . Yes, Delete ! As of this writing, the connector isn't smart enough to recognize that it couldn't write back to a read-only view and errored out. It also deleted records if it could. Perhaps this will be changed to provide a more refined control for the developer.

The second tab of the DCR contains general options for the connection. They are as follows :

• Max Number of Concurrent Connections
• Block Keyfield Updates
• Only Update Changed Fields
• Enable Conflict Detection
• Space Trimming
• Action on Data Mismatch
• Action on Missing Record
• Custom Settings (different for each type)

Let's review each of these options one by one.

Concurrent connections improve the performance of database access by permitting more than one connection to access the data source at a time. However, all database system have a maximum number of concurrent connections that they can handle, and they also have an optimal number of concurrent connections as well. Complicating the matter are the frequency and type of data access required. On top of all of that, licensing typically comes into play because most companies do not purchase licenses for all users. Therefore, this setting should be set in conjunction with your DBAs ”they'll have a much better understanding of the big picture and of the impact of your application.

Blocking keyfield updates is checked by default. This is almost always a good one to leave as is. Keyfields on records really shouldn't change, and this option adds a layer of protection to make sure that they don't.

Similar to Notes replication, the Only Update Changed Fields option sends column updates only if the corresponding Notes field has been changed.

Enabling conflict detection, although useful, is tricky. It checks the back-end record to see whether it has changed since it was last updated by Notes. If there has been a change, any update to that record does not succeed. There are two things to be aware of with regard to this setting: (1) A person needs to exit completely out of document before he resaves it ”even if he saved it while viewing (this can be a major training issue), and (2) This feature does not function on the Web.

Space trimming is fairly self-explanatory ”it decides whether to trim spaces. If space trimming occurs, it happens only for non-key fields. It's the same as the Trim Trailing Spaces setting in DECS.

Action on Data Mismatch is the same as the DECS Data Integrity settings. It's worded differently, but the outcome is the same. You have three options: (1) Raise an error (that is, you do not accept any loss of precision nor do you permit truncation), (2) Permit precision loss (but not truncation), and (3) Permit truncation (which implies possible precision loss, and also implies that it cannot be done to a key field).

Another option in the DCR that's the same as its counterpart in DECS, but worded slightly differently, is Action on Missing Record. It's the same as the Missing External Records item on the DECS Activity. Three options are again available: (1) Create the record, (2) Ignore the error, and (3) Raise an error.

The last part of the second tab is the Custom Settings. Different types of connectors offer different features that can be customized. In our example, we're using an ODBC connection, and its only option is whether multithreading is allowed. Many ODBC drivers, particularly older ones, do not support multithreading.

Form Properties

Forms now have a new set of properties that link the form with a DCR. You'll find these properties at the bottom of the form's second tab (see Figure 22.23).

Figure 22.23. The form must be attached to a DCR as found at the bottom of the Form properties, tab two.

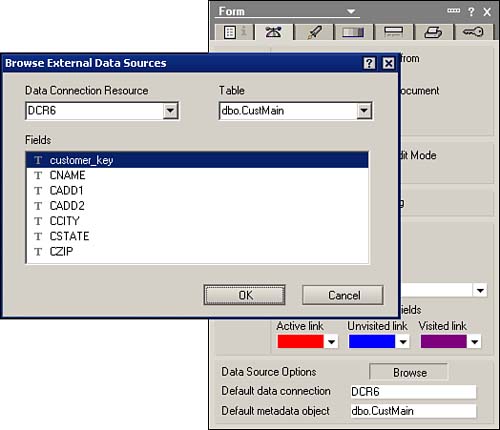
The only thing to do here is to pick from the list which DCR you'd like to link to your form. By clicking the Browse button, a list of DCRs appears. You can select the DCR that you like and then the elements in it. We did notice that, when selecting elements from the DCR (in particular Stored Procedures), we had to reselect the item if it defaulted to the one that we wanted. Note that these settings are the defaults for the form.

Field Properties

Fields have also been updated to provide a tighter integration between back-end databases and Notes. Of particular interest is the new External Data Source option, which is found under where you pick the type of field and whether it is multi-value . When you check that box, the Field Properties dialog box gets a little bit bigger at the bottom (see Figure 22.24).

Figure 22.24. The Field Properties dialog box, showing the new External Data Source option near the top and the new Data Source Options at the bottom.

After you've enabled the External Data Source setting for a field, you can then click the Browse button and select the DCR and Metadata object (these will default to what was selected in the form). You can then select the column on the back end that you want to map to this field on the front end.

When you've selected the DCR, the Metadata, and the External Field name, you're presented with two options: This Is a Key Field and This Is a Data Field.

If the particular field is a key field, its data will always be stored in the Notes document. If you select data field, you're given the option of storing the field both in Notes and in the back end.

NOTE

We've found that date fields and password fields are not permitted to be key fields ”only data fields. This somewhat hampers access based on date.