Tackling Nonlinear Systems of Equations

Problem

You have a system of nonlinear equations that you need to solve.

Solution

Frame the problem in terms of residuals and use Solver to minimize the residual, thus arriving at a solution.

Discussion

You can use the same Solver-based techniques discussed in Recipe 9.4 to solve systems of nonlinear equations. By way of example, consider the two equations:

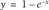
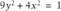
Let's assume you want to find a value, or values, of x satisfying both equations simultaneously. As you can see from the plot of these two equations shown in Figure 9-18, there are actually two solutions.

Figure 9-18. Nonlinear equations plot

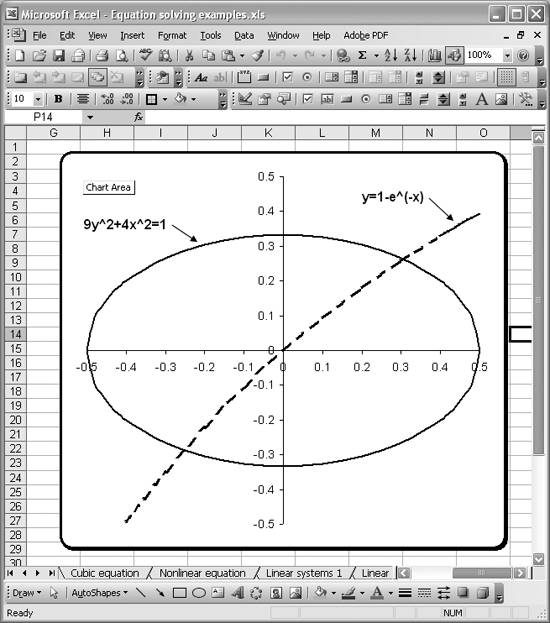
You have some choices as to how you approach a solution to this problem. If you can readily solve these equations for y (which you can in this case), then you can equate them and rewrite them in the form 0 = f(x) - g(x) and then use the techniques discussed in Recipe 9.2 to find a solution.

If you have more than two equations or you can't easily solve them in terms of a common variable, then you can use the minimization of residuals method discussed in Recipe 9.4, specifically in the section "Using Solver to minimize residuals," to find a solution. Using this latter approach, I found two xs that satisfy this system, namely, x = 0.306 and x = -0.253. In order to get Solver to find both solutions, I had to assume two different initial guesses for x. In one case I chose an initial x-value greater than 0.5, and in the other I chose an initial x-value less than -0.5.