Sparse Arrays

Suppose a city express bus runs down Main Street every ten minutes. To stay on schedule, it is supposed to stop at certain cross streets at certain times (Figure 12-11).

Figure 12-11. Schedule for the city express bus running down Main Street.

Cross Street	Time
2nd	:00
9th	:03
14th	:05
17th	:06
23rd	:09

We could represent this information using direct addressing: create an array of length 24, with the time for each stop at the appropriate index (Figure 12-12). All of the other elements of the array would be set to some other value, such as 1.

Figure 12-12. The bus schedule represented as a simple array. The shaded elements, where there are no stops, hold the value 1.

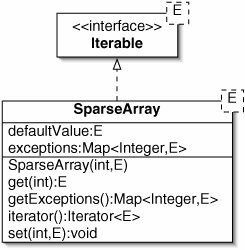
This works, but it wastes a lot of space. The problem is that the array is sparsealmost all of the elements have the same value. A better representation for a sparse array is to keep track of the exceptions to this default value using a Map (Figure 12-13). In our example this uses space linear in the number of stops, rather than in the number of cross streets.

Figure 12-13. UML class diagram of a proposed SparseArray class. The two arguments to the constructor are the size of the array and the default value.

This improved representation of sparse arrays can also increase speed. If we want to iterate through the stops, we don't have to waste time on the intervening streets. This idea of saving time by skipping over irrelevant data is worth remembering. We will see it again in Chapter 16.

Now suppose we have buses running up and down various streets and avenues of the city. We need to keep track of the locations of the stops within a two-dimensional grid. We could use the same idea as before, mapping two-dimensional coordinates to times. (More realistically, the value at each stop would be a Map itself, associating times with bus numbers.) This saves space over a simple array representation, but it does not allow us to easily traverse a single row or column.

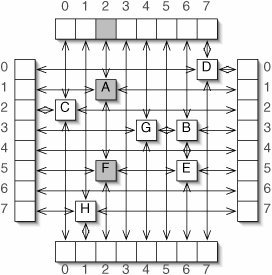
The solution to this problem is sketched in Figure 12-14. If we want to, for example, traverse column 2, we go to position 2 in the column header array across the top, then follow the chain of references down to the column footer array at the bottom. This visits only the exceptional elements in this column.

Figure 12-14. Conceptual drawing of a sparse, two-dimensional array. The arrays around the edges are headers and footers for the rows and columns. Only the shaded elements are examined in a top-down traversal of column 2.

(This item is displayed on page 337 in the print version)

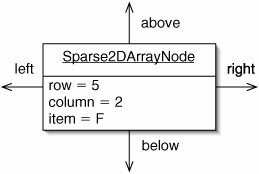
The individual exceptional elements are represented by quadruply linked list nodes (Figure 12-15). Each one knows its location as well as its neighbors above, below, to the left, and to the right. As in a doubly linked list, once we find such a node, we can remove it without having to know its predecessor. This is especially important here, because if we find a node by going down through a column, we don't want to have to search through the row to find its neighbor to the left.

Figure 12-15. A node in a sparse two-dimensional array is quadruply linked. It contains references to its neighbors in four directions. The neighbors themselves are not shown here.

(This item is displayed on page 337 in the print version)

Another advantage of this representation is that we can traverse a row or column in either direction.

Exercises

12.14

If the field exceptions in Figure 12-13 is a TreeMap, what is the order of the running time of the get() and set() methods?

Contiguous Representation of Multidimensional Arrays