The Comparable Interface

Our implementations of searching and sorting algorithms have dealt only with ints. It would be trivial to write similar versions for doubles.

Can we use polymorphism to write methods which will work on Objects? If so, we could use the same methods to search and sort structures containing Integers, Cards, or anything else.

This is not quite possible, because the notions of "greater than" and "less than" don't make sense for all classes. For example, what would it mean for one LinkedStack to be greater than another? What about graphic windows, customers, or sound clips?

It only makes sense to sort things which are comparable. Java provides a built-in interface Comparable. All of the wrapper classes, as well as String, implement Comparable (Figure 8-10).

Figure 8-10. Many classes implement the Comparable interface. The type parameter T simply stands for type. This name is somewhat arbitrary, but it doesn't make sense to talk about the "element" of a Comparable the same way we would talk about the elements of a List.

(This item is displayed on page 215 in the print version)

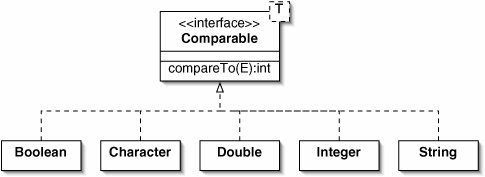
Comparable is generic because we can't compare instances of different subclasses. The type parameter specifies the class in question. Thus, Boolean implements Comparable, Character implements Comparable, and so on.

If we want a generic class to hold only instances of comparable classes, we must specify its type parameter as:

>

This means, "some class E that implements Comparable." In this context, Java does not distinguish between implementing an interface and extending a class; the keyword extends covers both cases.

For example, suppose we want an ArrayList that can only hold Comparables. We can create SortableArrayList, a subclass of ArrayList (Figure 8-11).

Figure 8-11. The class SortableArrayList is like ArrayList, but it can hold only Comparable objects.

1 /** An array-based List of Comparables. */
2 public class SortableArrayList>
3 extends ArrayList {
4 }

The Comparable interface specifies one method, compareTo(). This compares the current element to some other element and returns an int. Given two objects a and b, a.compareTo(b) returns a negative number if a is less than b, zero if a equals b, and a positive number if a is greater than b.

At first glance, this seems excessively complicated. Wouldn't it be clearer to supply three methods, isLessThan(), equals(), and isGreaterThan()?

It might be clearer, but it would be less efficient. There are many algorithms, such as binary search, where we need to do a different thing in each of these three cases. If we simply provided boolean methods, we would need to compare target with each array element twice (Figure 8-12). If the elements were large data structures (say, very long Strings corresponding to DNA sequences), this would be a lot of redundant computation.

Figure 8-12. A contains() method for the SortableArrayList class using binary search. If the Comparable interface specified separate methods isLessThan(), equals(), and isGreaterThan(), we would have to perform two comparisons in each pass through the loop. Comparable doesn't work this way, so this code is incorrect.

 1 public boolean contains(E target) {
 2 insertionSort();
 3 int bottom = 0;
 4 int top = size() - 1;
 5 while (bottom <= top) {
 6 int midpoint = (top + bottom) / 2;
 7 if (target.isLessThan(get(midpoint))) { // Illegal!
 8 top = midpoint - 1;
 9 } else if (target.equals(get(midpoint))) { // Illegal!
10 return true;
11 } else {
12 bottom = midpoint + 1;
13 }
14 }
15 return false;
16 }

With the single compareTo() method, we perform the comparison once, then examine the simple result of the comparison twice (Figure 8-13).

Figure 8-13. With the compareTo() method, we have to perform the potentially expensive comparison only once in each pass through the loop.

 1 public boolean contains(E target) {
 2 insertionSort();
 3 int bottom = 0;
 4 int top = size() - 1;
 5 while (bottom <= top) {
 6 int midpoint = (top + bottom) / 2;
 7 int comparison = target.compareTo(get(midpoint));
 8 if (comparison < 0) {
 9 top = midpoint - 1;
10 } else if (comparison == 0) {
11 return true;
12 } else {
13 bottom = midpoint + 1;
14 }
15 }
16 return false;
17 }

Incidentally, the compareTo() method in the String class uses lexicographical order to compare Strings. This is similar to alphabetical order, but it considers all upper-case letters to be earlier than all lower-case ones. It also handles nonalphabetic characters such as digits and punctuation marks, with the order specified by Unicode (which is identical to ASCII for common characters).

The contains() method in Figure 8-13 begins by insertion sorting the SortableArrayList. Code for this method is given in Figure 8-14.

Figure 8-14. The insertionSort() method for the SortableArrayList class.

 1 /** Arrange the elements in this List from smallest to largest. */
 2 public void insertionSort() {
 3 for (int i = 1; i < size(); i++) {
 4 E target = get(i);
 5 int j;
 6 for (j = i - 1;
 7 (j >= 0) && (get(j).compareTo(target) > 0);
 8 j--) {
 9 set(j + 1, get(j));
10 }
11 set(j + 1, target);
12 }
13 }

If we want to make one of our own classes Comparable, we have to declare that it implements Comparable and provide the compareTo() method. In some classes, this amounts to a simple subtraction. For example, Figure 8-15 shows a compareTo() method for the Die class from Chapter 1.

Figure 8-15. The compareTo() method for the Die class is a simple subtraction.

1 public int compareTo(Die that) {
2 return topFace - that.topFace;
3 }

When a class implements Comparable, the compareTo() method should be consistent with the equals() method. In other words, a.equals(b) should be true for exactly those values of a and b for which a.compareTo(b) returns 0.

Exercises

8.9	What is the value of "Z".compareTo("a")? (Note that the "Z" is upper case.)
8.10	Modify the Card class (Section 5.1) so that it implements Comparable.