Binary Search

We can take further advantage of the fact that an array is sorted by starting our search in the middle of the array. If we happen to find the target, we can return true immediately. If not, comparing the middle element to the target reveals whether the target belongs in the left or right half of the array. In other words, a constant amount of work allows us to divide the data in half. We then repeat this procedure until either we find the target or we run out of data. This algorithm, called binary search, is illustrated in Figure 8-2.

Figure 8-2. Binary search for 76 in a sorted array. Every time a number is compared to the target, half of the remaining array (shaded) is ruled out as a potential location.

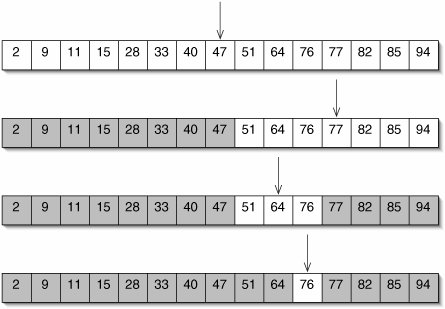
The code is given in Figure 8-3. The indices bottom and top specify the region of the array still under consideration. The loop shrinks this region until either the target is found or the region becomes empty.

Figure 8-3. In the binarySearch() method, each pass through the while loop on lines 514 rules out half of the array as a potential location for target.

 1 /** Return true if target appears in the sorted array data. */
 2 public static boolean binarySearch(int[] data, int target) {
 3 int bottom = 0;
 4 int top = data.length - 1;
 5 while (bottom <= top) {
 6 int midpoint = (top + bottom) / 2;
 7 if (target < data[midpoint]) {
 8 top = midpoint - 1;
 9 } else if (target == data[midpoint]) {
10 return true;
11 } else {
12 bottom = midpoint + 1;
13 }
14 }
15 return false;
16 }

Analysis of Binary Search

The running time of binary search is proportional to the number of times the loop runs. This is the number of times we have to divide the data in half before we run out of data.

We assume that n, the length of the array, is an exact power of 2. We will justify this shortcut in a moment. When we examine the middle element (or as close as we can get, given that n is even), one side of the array has n/2 elements and the other side has (n/2) 1 elements. In the worst case, we always have to look in the larger piece.

For example, if n = 8, we have one pass where there are 8 candidate elements, one where there are 4, one where there are 2, and one where there is 1. This is four passes. Notice that 23 = 8. If n were 24 = 16, we would need 5 passes.

The number of passes through the loop is p + 1, where 2p = n. The number p is, by definition, the base 2 logarithm of n. It is helpful to think of a base 2 logarithm as the number of times a number has to be divided in half before it gets down to 1 (Figure 8-4). We need p + 1 passes here because, after we get the search region down to a single element, we have to compare that last element to the target.

Figure 8-4. The base 2 logarithm of n is the number of times we have to divide n in half to get down to 1.

(This item is displayed on page 209 in the print version)

In the worst-case, then, the number of passes through the loop is 1 + log2 n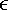

Assuming n Is a Power of Two

We do not generally expect n to be a power of two, but for most running-time functions this shortcut will not change the order of our result.

Theorem: Let f(n) and g(n) be two monotonically nondecreasing functions. If f(n) = g(n) for exact powers of two, and cg(n) > g(2n) for some constant c, then f(n) 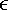O(n)) and f(n)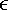

(This item is displayed on page 210 in the print version)

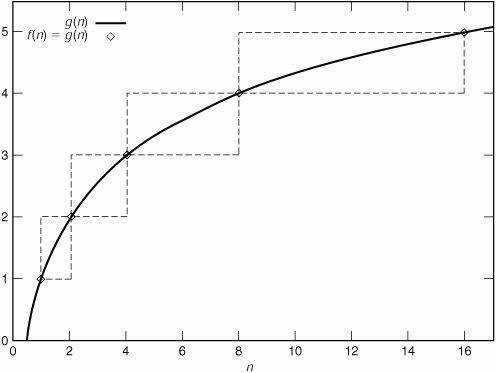
The functions are known to be equal at the marked points. Between these points, f(n) must stay within the dashed boundary. If it did not, it would have to decrease at some point. Since both functions are monotonically nondecreasing, this cannot happen.

To see that f(n) O(n)), consider the function cg(n). We know that cg(2) > g(4), cg(4) > g(8), and so on. In terms of the graph, cg(n) is always above the boundary boxes, and therefore greater than f(n). In other words, f(n) O(n)) = O(g(n)).

By a similar argument, f(n) log2

In general, the number of passes is 1 + log2 . The notation images/U230A.jpg border=0>, read "x," means "x rounded down to the nearest integer." Analogously, 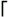, read "x," means "x rounded up to the nearest integer." Since log2 n is an integer for exact powers of 2, assuming that n is a power of 2 allows us to ignore floors and ceilings.

Exercises

8.3	In the analysis of binary search, we assumed that n is a power of 2. This means that n is even (unless it is 1), so there is no middle element. Which element does binary-Search() examine first?
8.4	The analysis of binary search given in this section is for a worst-case successful search, where we find the target just before we run out of places to look. What is the order of the running time for an unsuccessful search?
8.5	Instead of assuming that n is a power of 2, it is sometimes useful to assume that n is even. Prove that this is a safe thing to do.

Insertion Sort