C.4. Sums of Halves and Doubles

In the next formula, each term is half as large as the previous term.

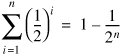
Even when we don't know the exact number of terms, we can still say:

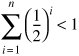
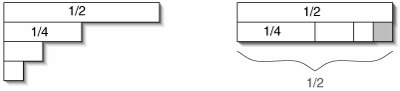
It may be somewhat surprising that the sum is less than 1 no matter how many terms there are. Figure C-3 shows why this is true.

Figure C-3. When the terms of a sum of halves are rearranged, they don't quite fill up a 2 x 1/2 rectangle. The missing piece is precisely the size of the last term: 1/2n.

It is sometimes more convenient to write a sum in which each term is twice (rather than half) the previous term.

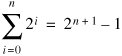
C 5 Upper Limit on Sum of a Function