Quicksort

Quicksort (by convention, the name is all one word, capitalized) is another divide-and-conquer sorting algorithm. In merge sort, the dividing was trivial. We simply took the left and right halves of the region being sorted. All of the hard work was done in recombining the sorted pieces by merging. In Quicksort, the hard work is in the dividing and the recombining is trivial.

Here's the plan:

1. If there are one or fewer numbers to sort, do nothing.
2. Otherwise, partition the region into "small" and "large" numbers, moving the small numbers to the left end and the large numbers to the right. Recursively sort each section. The entire array is now sorted.

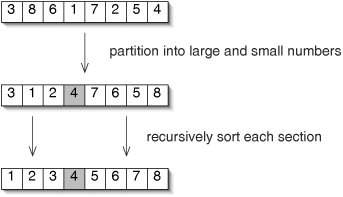
The process is illustrated in Figure 9-24.

Figure 9-24. Quicksort works by dividing the array into "small" and "large" numbersin this case, numbers less than or equal to 4 and numbers greater than 4. Each section is then recursively sorted.

As in merge sort, the primary methods are very short and elegant (Figure 9-25).

Figure 9-25. The methods quicksort() and quicksortHelper().

 1 /** Arrange the numbers in data from smallest to largest. */
 2 public static void quicksort(int[] data) {
 3 quicksortHelper(data, 0, data.length - 1);
 4 }
 5
 6 /**
 7 * Arrange the numbers in data between indices bottom and top,
 8 * inclusive, from smallest to largest.
 9 */
10 protected static void quicksortHelper(int[] data, int bottom,
11 int top) {
12 if (bottom < top) {
13 int midpoint = partition(data, bottom, top);
14 quicksortHelper(data, bottom, midpoint - 1);
15 quicksortHelper(data, midpoint + 1, top);
16 }
17 }

All of the hard work is done in the helper method partition(). The partitioning algorithm begins by choosing some array element as the pivot. We arbitrarily choose the last number in the region being partitioned as the pivot (Figure 9-26). Numbers less than or equal to the pivot are considered small, while numbers greater than the pivot are considered large. As it runs, the algorithm maintains four regions: those numbers known to be small, those known to be large, those which haven't been examined yet, and the pivot itself.

Figure 9-26. The partitioning algorithm chooses one number as the pivot. Four regions are maintained: small numbers, large numbers, unexamined numbers, and the region containing the pivot. The algorithm's last action is to swap the pivot into place between the small and large numbers.

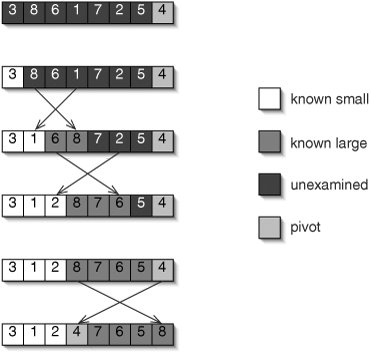
Working from left to right, each unexamined number is compared to the pivot. If it is large, the region of large numbers is simply extended. Otherwise, the newly discovered small number is swapped with the first known large number (if there are any) to keep all of the small numbers together. This continues until there are no unexamined numbers left. Finally, the pivot is swapped with the first large number (if any), so that it is between the small and large numbers.

The partition() method and its helper swap() are shown in Figure 9-27.

The number of variables in partition() make it appear complicated, but they are only there to maintain the four regions. Specifically:

• data[bottom] through data[firstAfterSmall - 1] are known to be small.
• data[firstAfterSmall] tHRough data[i - 1] are known to be large.
• data[i] tHRough data[top - 1] have not yet been examined.
• The pivot is at data[top].

Figure 9-27. The methods partition() and swap().

 1 /**
 2 * Choose one element of data in the region between bottom and top,
 3 * inclusive, as the pivot. Arrange the numbers so that those less
 4 * than or equal to the pivot are to the left of it and those
 5 * greater than the pivot are to the right of it. Return the final
 6 * position of the pivot.
 7 */
 8 protected static int partition(int[] data, int bottom, int top) {
 9 int pivot = data[top];
10 int firstAfterSmall = bottom;
11 for (int i = bottom; i < top; i++) {
12 if (data[i] <= pivot) {
13 swap(data, firstAfterSmall, i);
14 firstAfterSmall++;
15 }
16 }
17 swap(data, firstAfterSmall, top);
18 return firstAfterSmall;
19 }
20
21 /** Swap the elements of data at indices i and j. */
22 protected static void swap(int[] data, int i, int j) {
23 int temp = data[i];
24 data[i] = data[j];
25 data[j] = temp;
26 }

The index firstAfterSmall is the index of the first element that is not known to be small. When we swap element firstAfterSmall with element i on line 13, we are usually swapping element i with the first known large number. If there are no known large numbers yet, firstAfterSmall equals i, so we simply swap the element with itself; as desired, this has no effect.

Similarly, on line 17, firstAfterSmall is the index of either the first large number or (if there are no large numbers) the pivot. In either case, swapping the pivot into this position is correct.

Analysis of Quicksort

An invocation of partition() takes time linear in the length of the array being sorted, because there are n passes through the loop. What about quicksortHelper()? Partitioning a region of size n as evenly as possible, we might end up with small numbers and images/U230A.jpg border=0> large numbers. We ignore the floor and ceiling by assuming that

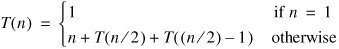
Since this is strictly less than the recurrence for merge sort, it is tempting to conclude that quicksort takes time in O(n log n). While this is true in the best case, partition() might not divide the region evenly in half. In the worst case, there might be no large numbers. For example, if the array is already sorted, the number we choose as the pivot is the largest element. There are then n 1 numbers to the left of the pivot and none to the right. In this case, the recurrence is:

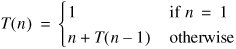
The solution to this recurrence is:

Quicksort takes quadratic time in the worst case.

While the analysis is beyond the scope of this book, it turns out that Quicksort takes time in Q(n log n) in the average case. Quicksort is therefore better than insertion sort, but not as good as merge sort.

Since it has a low constant factor associated with its running time, and operates in place, Quicksort is sometimes used instead of merge sort when n is not expected to be very large. There are also a number of minor changes (see the Exercises) which can be made to the algorithm to greatly decrease the likelihood of the worst-case running time.

The class java.util.Arrays has several overloaded versions of the static method sort(). The ones for arrays of primitive types use an optimized version of Quicksort that makes the worst-case behavior unlikely. The version for arrays of objects uses merge sort. The difference has to do with the fact that two objects that are equals() may not be identical. For example, two Cards with the same rank but different suits are equals(). If a sort keeps such elements in the same order as in the original array, the sort is said to be stable. Merge sort is stable, but Quicksort is not. Since equal primitives must be absolutely identical, stability is not an issue when sorting primitives.

Exercises

9.13	What is the order of the running time of Quicksort if data is originally in reverse sorted order? What if all the elements are identical?
9.14	Add a quicksort() method to the SortableArrayList class from Section 8.4.
9.15	Modify quicksortHelper() so that, before invoking partition(), it swaps a random element in the region being sorted with the last element. With this change, no particular input can consistently produce the worst-case behavior.
9.16	Suppose the variable numbers, of type List, contains many numbers in no particular order. How can it be sorted in one line of code? (Hint: See the java.util.Collections class in the API.)