Hash Tables

The third and final implementation of the Set interface presented in this chapter is the hash table. Before explaining hash tables proper, we take a brief detour to write the LetterCollection class for the Anagrams game.

Direct Addressing

A LetterCollection is, not surprisingly, a collection of letters. Put another way, it requires that we know how many of each letter are in the collection. Since there are only 26 different letters, this does not require a data structure as complicated as an ordered list or a binary search tree. All we need is an array of 26 ints, one for each letter (Figure 11-29). It is also handy to keep track of the total number of letters in the collection.

Figure 11-29. UML instance diagram of a LetterCollection containing one 'a', three 'd's, and one 'y'. While there isn't room to show it, the array has 26 elements.

(This item is displayed on page 306 in the print version)

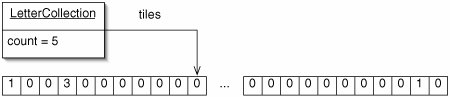
If we want to know, for example, how many 'd's are in a LetterCollection, we look at the appropriate element of the array tiles. To find the index, we take advantage of the fact that, in Java, we can do arithmetic on chars. If we have a char letter, the index we want is letter 'a'. This expression gives 0 if letter is 'a', 1 if it is 'b', and so on.

The code is given in Figure 11-30. When invoked with the argument TRue, the constructor creates a LetterCollection containing letters in proportion to their frequency in English text. For example, there are 50 'e's, but only 3 'q's.

Figure 11-30. The LetterCollection class.

 1 /** Collection of letters for use in Anagrams. */
 2 public class LetterCollection {
 3
 4 /** Total number of letters. */
 5 private int count;
 6
 7 /**
 8 * Number of each letter. For example, tiles[0] is the number of
 9 * 'a's.
10 */
11 private int[] tiles;
12
13 /**
14 * If full is true, there are 416 letters, with more copies of
15 * more common letters like 'e'. Otherwise, the new
16 * LetterCollection is empty.
17 */
18 public LetterCollection(boolean full) {
19 if (full) {
20 tiles = new int[] {29, 5, 12, 16, 50, 9, 8, 20, 28,
21 4, 5, 16, 9, 30, 28, 8, 3, 30,
22 24, 36, 14, 8, 8, 4, 9, 3};
23 count = 416;
24 } else {
25 tiles = new int[26]; // All zeroes
26 count = 0;
27 }
28 }
29

30 /** Add a single letter to this LetterCollection. */ 31 public void add(char letter) { 32 tiles[letter - 'a']++; 33 count++; 34 } 35 36 /** Add each letter in word to this LetterCollection. */ 37 public void add(String word) { 38 for (char c : word.toCharArray()) { 39 tiles[c - 'a']++; 40 } 41 count += word.length(); 42 } 43 44 /** Remove and return a random letter. */ 45 public char draw() { 46 int rand = (int)(Math.random() * count); 47 for (int i = 0; i < 26; i++) { 48 if (rand < tiles[i]) { 49 tiles[i]--; 50 count--; 51 return (char)('a' + i); 52 } else { 53 rand -= tiles[i]; 54 } 55 } 56 return '?'; // This should never happen 57 } 58 59 /** Remove each letter in word from this LetterCollection. */ 60 public void remove(String word) { 61 for (char c : word.toCharArray()) { 62 tiles[c - 'a']--; 63 } 64 count -= word.length(); 65 } 66 67 public String toString() { 68 String result = ""; 69 for (int i = 0; i < 26; i++) { 70 for (int j = 0; j < tiles[i]; j++) { 71 result += (char)('a' + i); 72 } 73 } 74 return result; 75 } 76 77 }

On lines 3840 and 6062, we use enhanced for loops to traverse Strings. Strings do not support enhanced for loops (an apparent oversight in Java 1.5), but arrays of chars do, so we use the toCharArray() method in the String class.

We could use a similar data structure to represent a set of chars. Remember that the difference between a set and a collection is that the same item cannot appear more than once in the same set. Instead of an array of ints, then, we would need only an array of booleans.

In either case, this approach is called direct addressing. When we want to look up some element, we go directly to the appropriate place in the array. Direct addressing should be used wherever it is applicable, because it is incredibly fast: looking up an element takes constant time.

Hash Functions and Hash Codes

Unfortunately, direct addressing cannot be used for every set. The first problem is that the set of possible elements might be vastly larger than the set of elements actually stored. For example, suppose an employer is storing a set of employee Social Security numbers. There are a billion possible nine-digit Social Security numbers, but no company has anywhere near this many employees. A direct addressing table would be a huge waste of space.

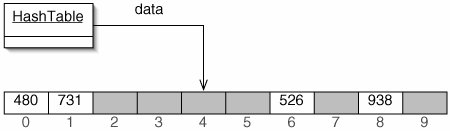
This problem is solved using a hash function. This is a function which takes an int as input and returns an array index. For example, we might use the function f(x) = x mod 10. Figure 11-31 shows several three-digit numbers stored in an array of length 10. If we want to store 526 in the array, we put it at position 526 mod 10 = 6. We store the number there, rather than merely a boolean value of true, because more than one number "hashes to" this position.

Figure 11-31. In a hash table, a hash function maps each potential element to an array index. The shaded positions do not contain set elements; in practice, some invalid value such as 1 or null is stored there.

This design, called a hash table, appears to have all of the advantages of direct addressing, even though it works when the number of possible elements is much larger than the number of elements actually stored. There are, of course, some complications.

First, the elements to be stored might not be integers. Most of the built-in classes of which we are likely to store Sets (String, Integer, Double, etc.) have a method hashCode() which takes no arguments and returns an int which can be passed to a hash function. This int is called the hash code.

The hashCode() method must return the same value for two objects which are equals(). The converse is not true, though: if a.hashCode() == b.hashCode(), it does not follow that a.equals(b). Sometimes two different, nonidentical objects have the same hash code.

If we want to store instances of one of our own classes in a hash table, we must define both equals() and hashCode(). This is necessary because the hash table Set methods use hashCode() to find the right position in the table, then use equals() to verify that the item at that position is the one we're looking for. If these methods don't provide consistent results, the hash table might give an incorrect result when asked if some object is in the Set.

Different objects sometimes produce the same hash code. Furthermore, even if they didn't, the hash function might occasionally map two different hash codes to the same index. For example, 37 mod 10 = 87 mod 10. This is called a collision.

We try to choose a hash function which makes collisions rare. If our hash codes tend to be even numbers, then f(x) = x mod 10 is a bad hash function, because more elements will be put at the even positions than at the odd positions. A better choice is f(x) = x mod s, where s is some prime number. This tends to disrupt any patterns in the data. This is where the data structure gets its name: "to hash" means "to chop up and mix around."

No matter how good our hash function is, collisions cannot be completely avoided. Since there are more potential elements than positions in the table, some elements must hash to the same location. This is the pigeonhole principle: if there are n pigeonholes and more than n pigeons, at least one hole will have more than one pigeon. We now discuss a number of techniques for dealing with collisions.

Collision Resolution

The first approach, called chaining, is to keep a sequence of ListNodes (effectively an ordered list) at each position in the table (Figure 11-32). To search, insert, or delete, we simply use the hash function to find the right list and then perform the appropriate ordered list operation there.

Figure 11-32. In a hash table with chaining, each position in the array contains an ordered list of elements that hash to that index.

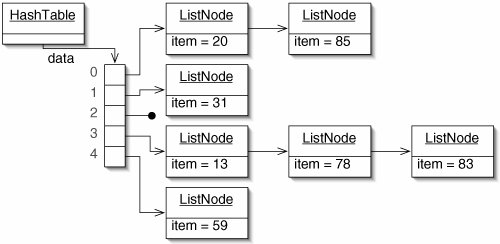
If we know in advance how many elements the Set contains (n), we can choose the array length to be proportional to thissay, 2n. This limits the average number of elements per list to a constant, in this case 1/2. While all of the data could end up in the same list if we were very unlucky with our hash function, the average time for search, insertion, and deletion is Q(1). This is an astounding result: the time to perform a search is independent of the size of the set!

Chaining works, but all of the references involved in such a linked structure take up considerable space. The two remaining collision resolution techniques avoid this by storing all of the elements directly in the array. This is called open addressing. While the analysis is beyond the scope of this book, hash tables using open addressing have performance in the same order as hash tables using chaining.

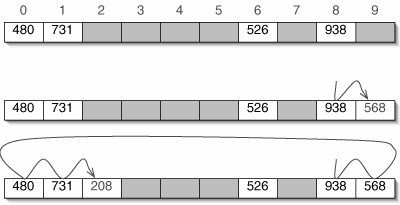
The first open addressing technique is linear probing (Figure 11-33). If there is a collision during insertion, we simply move on to the next unoccupied position. If this would move us past the end of the array, we wrap around to the beginning.

Figure 11-33. Linear probing. For simplicity, only the array is shown here. The original array is at the top. When 568 is inserted (middle), it hashes to position 8, which is occupied, so the next position is used. When 208 is inserted (bottom), positions 8, 9, 0, and 1 must be tried before the empty position 2 is found.

There are three problems with linear probing:

• The table can fill up. With chaining, if we underestimate the number of elements in the set, the lists get longer and search is slower. With linear probing, the hash table fails catastrophically: when there's no more room, we simply can't insert any more elements.

  We can solve this problem by rehashing when the table gets too full. Rehashing is copying all of the elements into a fresh table. If we make the new table larger, as we did with our ArrayList class, the new table is not full.

• We can't simply remove an item to delete it. In Figure 11-33, suppose we removed 480 and then searched for 208. We would hit an unoccupied position and incorrectly conclude that 208 is not in the table.

  We get around this problem by replacing a deleted item with a special value deleted. This is neither null nor is it equals() to any target, so searches continue past it. This in turn creates another problem: the table may become full of deleteds, with very few actual data elements. This, too, can be solved by occasionally rehashing.

• Clusters of contiguous occupied positions tend to occur and grow (Figure 11-34). Once a cluster appears, an element which hashes to a position in the cluster may result in a linear search to the end of the cluster. Worse, an insertion into any position in a cluster expands the cluster.

Figure 11-34. Linear probing can result in clusters. In this table, the shaded positions are unoccupied. Any new element is 25% likely to end up in the large cluster near the right end, which both slows down search and expands the cluster.

The problem of clustering is reduced by a second open addressing technique, double hashing. In double hashing, we use two hash functions. The first function tells us where to look first, while the second one tells us how many positions to skip each time we find an occupied one (Figure 11-35). If we choose our two hash functions well, two elements which originally hash to the same position are unlikely to follow the same sequence of positions through the table. This reduces the risk of clustering. Note that linear probing is a special case of double hashing, where the second hash function always returns 1.

Figure 11-35. Double hashing reduces clustering. In this table, the first hash function is f(x) = x mod 10 and the second hash function is g(x) = images/U230B.jpg border=0>. When 256 is inserted, we first look in position 6 and then every 2 positions thereafter. When 386 is inserted, we again start at position 6, but then proceed 3 positions at a time.

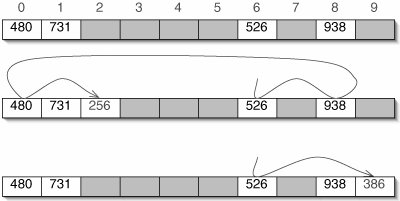
It is crucial that the size of the table and the number returned by the second hash function be relatively primethat is, have no factors in common other than 1. To see why, suppose we have an array of length 10 and the second hash function returns 5. A search that begins at position 7 will go to position 2, then back to 7. Only two positions are checked before the algorithm gives up and incorrectly concludes that the table is full!

The easiest way to ensure relative primality is to make the table size a power of two, then require that the second hash function always returns an odd number.

We now present an implementation of hash tables using double hashing. The basics are shown in (Figure 11-36). The constructor requires some instance of the generic type E to use for deleted. In the hash functions, we have to use the absolute value function Math.abs() because hashCode() is not guaranteed to return a nonnegative number and % does not work as modulo if its first argument is negative.

Figure 11-36. Easy parts of the HashTable class.

1 /** A hash table of Comparables, using double hashing. */ 2 public class HashTable implements Set { 3 4 /** 5 * Special object to indicate a slot previously occupied by a 6 * Comparable. 7 */ 8 private E deleted; 9 10 /** Comparables stored in this table. */ 11 private E[] data; 12 13 /** Number of occupied slots (including deleteds). */ 14 private int fullness; 15 16 /** 17 * A HashTable is initially empty, but an initial capacity may 18 * be specified. 19 */ 20 public HashTable(E deleted) { 21 data = (E[])(new Object[1]); // All null; compiler warning 22 fullness = 0; 23 this.deleted = deleted; 24 } 25 26 /** First hash function. */ 27 protected int hash1(E target) { 28 return Math.abs(target.hashCode()) % data.length; 29 } 30 31 /** Second hash function. */ 32 protected int hash2(E target) { 33 int result = Math.abs(target.hashCode()) % (data.length - 1); 34 if (result % 2 == 0) { return result + 1; } 35 return result; 36 } 37 38 public int size() { 39 int tally = 0; 40 for (E item : data) { 41 if ((item != null) && (item != deleted)) { 42 tally++; 43 } 44 } 45 return tally; 46 } 47 48 }

Search

To search (Figure 11-37), we use hash1() to decide where to start. If this position is occupied by something other than target, we use hash2() to decide how many positions to skip ahead. This continues until we get back to the beginning, find a null slot, or find target.

Figure 11-37. The contains() method.

 1 public boolean contains(E target) {
 2 int start = hash1(target);
 3 int i = start;
 4 while (data[i] != null) {
 5 if (target.equals(data[i])) {
 6 return true;
 7 }
 8 i = (i + hash2(target)) % data.length;
 9 if (i == start) {
10 return false;
11 }
12 }
13 return false;
14 }

Insertion

Insertion (Figure 11-38) is almost identical to search, followed if necessary by installing target. It may also be necessary to rehash. In our implementation, if the table is at least half full (including deleteds), we rehash into a larger table before inserting. As in our ArrayList class, we double the capacity of the table when we stretch it, so the amortized time for rehashing is still constant.

Figure 11-38. The add() and rehash() methods.

 1 public void add(E target) {
 2 if (fullness >= data.length / 2) {
 3 rehash();
 4 }
 5 int start = hash1(target);
 6 int i = start;
 7 while (data[i] != null) {
 8 if (target.equals(data[i])) {
 9 return;
10 }
11 i = (i + hash2(target)) % data.length;
12 if (i == start) {
13 return;
14 }
15 }
16 data[i] = target;
17 fullness++;
18 }
19
20 /**
21 * Copy all of the elements into a new array twice as large.
22 */
23 public void rehash() {
24 HashTable newTable = new HashTable(deleted);
25 newTable.data = (E[])(new Object[data.length * 2]);
26 for (int i = 0; i < data.length; i++) {
27 if ((data[i] != null) && (data[i] != deleted)) {
28 newTable.add((E)(data[i]));
29 }
30 }
31 data = newTable.data;
32 fullness = newTable.fullness;
33 }

Deletion

In remove() (Figure 11-39), we replace target with deleted if we find it.

Where applicable, hash tables are far and away the best Set implementation. The average running times for search, insertion, and deletion are constant. The worst case is linear, but this is not nearly as likely to occur with hash tables as it is with binary search trees.

Figure 11-39. The remove() method.

 1 public void remove(E target) {
 2 int start = hash1(target);
 3 int i = start;
 4 while (data[i] != null) {
 5 if (target.equals(data[i])) {
 6 data[i] = deleted;
 7 return;
 8 }
 9 i = (i + hash2(target)) % data.length;
10 if (i == start) {
11 return;
12 }
13 }
14 }

There are only two drawbacks to hash tables. First, traversal is not efficient. Visiting all of the elements requires a search through the entire table, which is presumably mostly empty. This takes time proportional to the capacity of the table, not to the number of elements. Second, with open addressing, deletion is a bit awkward; we have to leave behind a special value deleted and occasionally rehash. A hash table may not be the best Set implementation to use in an application where many deletions are expected.

Exercises

11.12	Analyze the worst-case running times of the methods in the LetterCollection class. Give your results in terms of n, the size of the set, and (where appropriate) w, the length of the word involved.
11.13	Consider two instances a and b of some class. If a.hashCode() == b.hashCode(), does it follow that a.compareTo(b) == 0? What about vice versa? Explain.
11.14	Why can't we simply use public int size() { return fullness; }   for the size() method in the HashTable class?
11.15	What would happen if someone invoked add(null) on a HashTable as defined in this section? Write an assertion to prevent this.
11.16	We need to use the special values null and deleted to keep track of unoccupied positions in the table. Devise and explain another way to keep track of these things, so that we could store null as a member of the Set and we wouldn't need to specify a value for deleted when invoking the constructor.
11.17	Which approach would have better cache performance: chaining or open addressing? Explain.
11.18	Modify the code in Figure 11-36 so that the HashTable uses linear probing instead of double hashing. (Hint: Only one method has to be modified.)
11.19	Assuming a good hashCode() method and a good hash function, an element chosen at random is equally like to hash to any position in the table. What is the probability that two elements chosen at random hash to the same location?
11.20	Suppose we perform 1,000 insertions followed by 900 deletions in a HashTable as defined in this section, then rehash. In what sense is the resulting data structure inefficient?
11.21	The HashTable class defined in this section can store only Comparable objects, because it implements the Set interface. What would we have to change to allow a HashTable to store objects of any class? Would this same idea work for the OrderedList and BinarySearch classes? Explain.

The Java Collections Framework Again