The Call Stack

Figure 4-15 shows a program for computing the length of the hypotenuse of a right triangle, given the lengths of the other two sides.

Figure 4-15. To keep things simple, all of the methods in the Hypotenuse class are static.

 1 /** Compute the hypotenuse of a right triangle. */
 2 public class Hypotenuse {
 3
 4 /** Return the square of the number x. */
 5 public static double square(double x) {
 6 return x * x;
 7 }
 8
 9 /**
10 * Return the hypotenuse of a right triangle with side lengths x
11 * and y.
12 */
13 public static double hypotenuse(double x, double y) {

14 double x2 = square(x); 15 double y2 = square(y); 16 return Math.sqrt(x2 + y2); 17 } 18 19 /** Test the methods. */ 20 public static void main(String[] args) { 21 double result = hypotenuse(3, 4); 22 System.out.println(result); 23 } 24 25 }

The hypotenuse() method invokes the square() method twice: once on line 13 and once on line 14. When Java finishes an invocation of square(), how does it know where to go next? Should it invoke square() again or go on to Math.sqrt()?

The vague answer is that Java somehow "keeps track of" what it was doing before the invocation started. How? Using a stack.

This stack, called the call stack, exists behind the scenes. It is not an object that we can access, but we can understand it now that we know about stacks.

Every time a method is invoked, a behind-the-scenes object called a call frame is created. The call frame keeps track of the current state of the method. Specifically, it stores any arguments or variables for the method. It also keeps track of how far along the method has proceeded.

The history of the call stack for this program is illustrated in Figure 4-16. When Java first starts up, the call stack is empty. When main() is invoked, a new call frame is created and pushed onto the stack. This call frame stores the value of args (which we ignore in this example) and result, as well as the fact that we are at the beginning of the main() method (that is, line 20). (The author has carefully crafted the Hypotenuse program so that only one method invocation happens on each line. In a more complicated program, Java would break each line into multiple steps.)

Figure 4-16. History of the call stack for the Hypotenuse program.

(This item is displayed on page 99 in the print version)

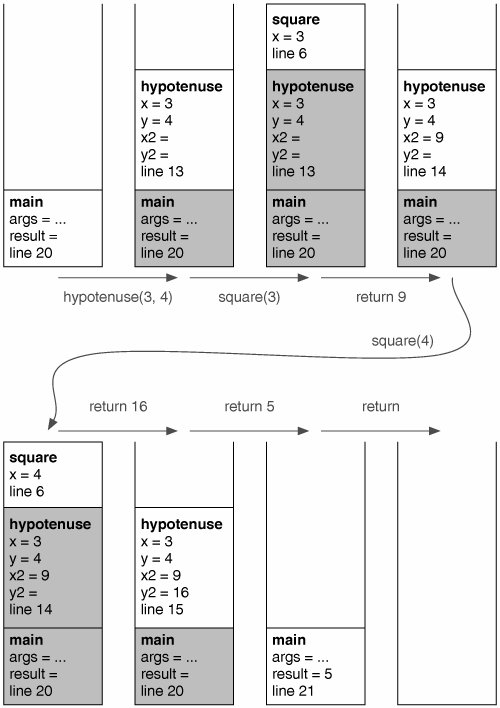
On line 20, the main() method invokes hypotenuse(3, 4). Java creates a call frame for hypotenuse() and pushes it onto the stack. In this new call frame, x is 3, y is 4, and the method is at the beginning, on line 13. The variables x2 and y2 have not yet been initialized.

The hypotenuse() method then needs square(3), which causes yet another call frame to be pushed onto the stack. At any point, only the top frame on the call stack is active. The others are waiting for answers from methods they invoked. This clears up any confusion between arguments and variables with the same name in different methods, or in different invocations of the same method.

When square() finishes, its call frame is popped off the stack. The next frame down, the invocation of hypotenuse(), stores the returned value 9 in the variable x2 and moves on to ask for square(4).

Eventually, main() finishes, the last call frame is popped off the stack, and the program is done.

This was a lot of work, and we can be thankful that Java does it for us. We normally don't even have to think about the call stack, although it will be useful knowledge when we discuss recursion in Chapter 9.

Knowledge of the call stack also helps us understand some of Java's error messages. Suppose we are playing Idiot's Delight and decide to deal out all of the cards before discarding any. Unfortunately, we aren't paying attention to the number of cards left and we try to deal from any empty deck. The program crashes with a message like the one shown in Figure 4-17.

Figure 4-17. Stack trace in an error message from Java.

1 Exception in thread "main"
2 java.lang.ArrayIndexOutOfBoundsException: -1
3 at Deck.deal(Deck.java:25)
4 at IdiotsDelight.deal(IdiotsDelight.java:24)
5 at IdiotsDelight.play(IdiotsDelight.java:58)
6 at IdiotsDelight.main(IdiotsDelight.java:81)

The error message shows a stack trace (a snapshot of the call stack) indicating what was going on when the program crashed. The actual error occurred in the deal() method of the Deck class, so the top call frame was an invocation of this method. It was invoked in line 24 of the deal() method from the IdiotsDelight class, which was invoked on line 58 of the play() method, which was invoked on line 81 of the main() method. (These line numbers are from the complete files, so they won't match the numbers in our figures. Your numbers may differ due to whitespace, comments, and so on.)

Examining a stack trace makes our debugging much easier, because we can immediately tell that the deal() method from Deck either contains a bug or (as in this example) was called inappropriately. The next section discusses how to deal with such bad input without crashing the program.

Exercises

4.5	Can two call frames ever be waiting for each other? Explain.
4.6	Every method invocation involves pushing a frame onto the call stack, which takes up time and memory. Discuss whether we should avoid this by writing every program in a single, monolithic main() method.