Topological Sorting

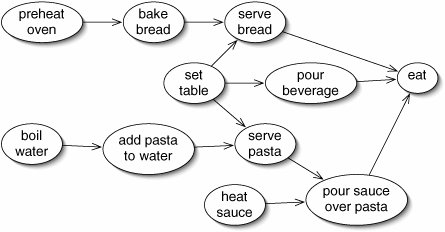
A directed acyclic graph can be used to represent a set of tasks, some of which are prerequisites of others (Figure 15-23). An edge indicates that one task must be performed before another.

Figure 15-23. Dinner involves a number of different tasks, shown in this directed graph. An edge indicates that one task must be performed before another. For example, the oven must be preheated before the bread can be baked. It should be noted that only a programmer would consider this a complete meal.

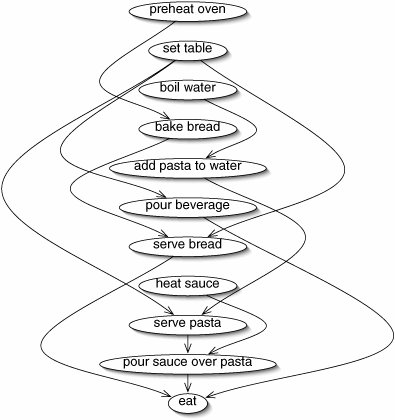
A topological sort of such a graph is an ordering in which the tasks can be performed without violating any of the prerequisites. There may be more than one topological sort of a given graph. If the graph is redrawn with all of the vertices in topologically sorted order, all of the arrows lead from earlier to later tasks (Figure 15-24).

Figure 15-24. When the vertices are arranged in topologically sorted order, all of the edges lead from earlier to later tasks.

For a second example, consider the game of Pick Up Sticks (Figure 15-25).

Pick Up Sticks

Players: 2 or more

Object: To pick up as many sticks as possible.

Setup: Drop a number of long, thin sticks in a disorganized pile on the ground.

Play: In turn, each player picks up a stick. If she successfully extracts a stick without moving any of the others, she wins that stick and gets another turn.

In practice, this is a game of dexterity. Ignoring this detail, we can phrase it as a topological sorting problem: in what order should the sticks be picked up? Before any stick can be picked up, all of the sticks overlapping it must be picked up. A topological sort is a valid order for picking up the sticks (Figure 15-26).

Figure 15-26. A game of Pick Up Sticks and the corresponding directed acyclic graph. An edge indicates that one stick overlaps another. A topological sort of this graph would give a valid order for picking up the sticks.

We would like to write a program that, given the information on which sticks overlap which other sticks, determines an order in which they may be picked up. A transcript is given in Figure 15-27.

The heart of this program is the topological sorting algorithm. This algorithm is similar to a series of depth-first traversals, one starting from each vertex, but all sharing the same visited array.

Figure 15-27. Transcript of the PickUpSticks program.

 1 Welcome to Pick Up Sticks.
 2
 3 How many sticks are there? 4
 4 Which sticks overlap stick 0 (separate with spaces)?
 5 Which sticks overlap stick 1 (separate with spaces)? 0
 6 Which sticks overlap stick 2 (separate with spaces)? 1 3
 7 Which sticks overlap stick 3 (separate with spaces)? 0
 8
 9 The sticks can be picked up in this order:
10 ( 0 3 1 2 )

Suppose we do a depth-first traversal starting from some vertex, such as vertex F in Figure 15-26. When we complete this traversal, we have visited everything that can be reached from this vertex. In other words, we have stick F and everything below it. If we add each vertex to the end of the solution list as we visit it, all of the edges will lead backward. If we add these vertices to the beginning instead, all of the edges will lead forward, giving us a topological sort.

The code is given in (Figure 15-28).

Figure 15-28. The topological sort algorithm performs a series of depth-first, postorder traversals. These methods are in the Graph class.

1 /** Return a topological sort of this directed acyclic Graph. */ 2 public List topologicalSort() { 3 LinkedList result = new LinkedList(); 4 boolean[] visited = new boolean[size()]; 5 for (int i = 0; i < size(); i++) { 6 if (!visited[i]) { 7 topologicalTraverse(i, result, visited); 8 } 9 } 10 return result; 11 } 12 13 /** 14 * Visit the vertices reachable from vertex in depth-first 15 * postorder, adding them to result. The array visited 16 * prevents any vertex from being visited more than once. 17 */ 18 protected void topologicalTraverse(int vertex, 19 LinkedList result, 20 boolean[] visited) { 21 visited[vertex] = true; 22 for (Integer i : neighbors(vertex)) { 23 if (!visited[i]) { 24 topologicalTraverse(i, result, visited); 25 } 26 } 27 result.setNext(new ListNode(vertex, result.getNext())); 28 }

Each vertex is visited exactly once. It takes time in Q(v) to traverse the neighbors of each vertex, so the total running time for topologicalSort() is in Q(v2).

The PickUpSticks program is now just a bit of input and output (Figure 15-29).

Figure 15-29. The PickUpSticks program.

 1 import java.util.Scanner;
 2
 3 /** The game of Pick Up Sticks. */
 4 public class PickUpSticks {
 5
 6 /** For reading from the console. */
 7 public static final Scanner INPUT = new Scanner(System.in);
 8
 9 /**
10 * Directed acyclic graph indicating which sticks overlap which
11 * others.
12 */
13 private Graph overlaps;
14
15 /** The number of sticks is set here, but not any overlaps. */
16 public PickUpSticks(int n) {
17 overlaps = new Graph(n);
18 }
19
20 /** Ask the user which sticks overlap which others. */
21 protected void determineOverlaps() {
22 for (int i = 0; i < overlaps.size(); i++) {
23 System.out.print("Which sticks overlap stick " + i
24 + " (separate with spaces)? ");
25 Scanner line = new Scanner(INPUT.nextLine());
26 while (line.hasNextInt()) {
27 overlaps.addEdge(line.nextInt(), i);
28 }
29 }
30 }
31

32 /** Print an order in which the sticks can be picked up. */ 33 protected void solve() { 34 System.out.println(" The sticks can be picked up in 35 + "this order:"); 36 System.out.println(overlaps.topologicalSort()); 37 } 38 39 /** Create and solve the game. */ 40 public static void main(String[] args) { 41 System.out.println("Welcome to Pick Up Sticks. "); 42 System.out.print("How many sticks are there? "); 43 PickUpSticks game = new PickUpSticks(INPUT.nextInt()); 44 INPUT.nextLine(); // To clear out input 45 game.determineOverlaps(); 46 game.solve(); 47 }

We do something unusual on lines 2426 to read several numbers on one line. We read in a line of text, store it in the String line, and then create a new Scanner that reads from that line instead of from the keyboard. We can read ints from this Scanner until there are none left. It wouldn't work to read these directly from the keyboard, because the Scanner would have no way of knowing when the user was done entering numbers.

Exercises

15.14	Give a topological sort of the graph at the bottom of Figure 15-26.
15.15	Draw the graph described in Figure 15-27.
15.16	In the topological sort algorithm, why is it important that the graph be acyclic? What would our topologicalSort() method do if given a cyclic graph?
15.17	Why is it more efficient for topologicalSort() to use a LinkedList rather than an ArrayList?
15.18	What is the running time of topologicalSort(), assuming a neighbor list representation?