Ordered Lists

The most obvious approach to implementing the Set interface is to use one of the linear structures introduced in Part II. Since a Set changes size as items are added and removed, a linked structure seems in order. In this section, we look at an ordered list, a data structure based on a linked list.

Many efficient Set implementations depend on the elements being Comparable (Section 8.4). We will therefore develop a class OrderedList for sets of such elements. An OrderedList is just like a LinkedList, except that:

1. The elements of an OrderedList must implement the Comparable interface.
2. The elements of an OrderedList are kept in order.
3. The OrderedList class implements the Set interface. It provides the methods add(), contains(), remove(), and size(). No duplicate elements are allowed.

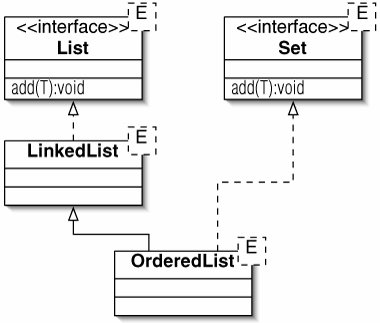
The words "just like ... except" suggest that OrderedList might extend LinkedList (Figure 11-8). The problem with this approach is that the LinkedList class implements the List interface, which conflicts with the Set interface. Specifically, the add() method from the List interface should add the argument target to the end of the list, even if it is already present, while the add() method from the Set interface may add target at any position, but not if it is already present. Since the add() method in OrderedList would override the one in LinkedList, an OrderedList would behave like a Set. As far as the Java compiler could tell, however, it would be a legitimate value for a variable of type List, because it would be a descendant of LinkedList.

Figure 11-8. It would be a bad idea for OrderedList to extend LinkedList, because it would then have to provide two conflicting add() methods.

(This item is displayed on page 292 in the print version)

To see why this is a problem, suppose OrderedList extended LinkedList. If someone executed the code

List livestock = new OrderedList();
livestock.add("llama");
livestock.add("llama");

then they might expect list.size() to return 2but it would return 1. A variable may be set to a reference to an object created very far away in the code (even in a different class), so this could lead to some extremely tricky bugs. We should extend a class only when an instance of the subclass works in place of an instance of the superclass.

Although we won't have OrderedList extend LinkedList, there's no reason not to cut and paste like crazy. Figure 11-9 shows the trivial parts of the OrderedList class. On line 2, the generic type E is constrained to be a Comparable type.

We now discuss the other three methods from the Set interface: contains(), add(), and remove(). This sequence will be followed for all three Set implementations in this chapter. Within each implementation, all three methods have very similar structures. This happens because, to add something to a Set, we must first find where it belongs, then (if it is not present) put it there. To remove something, we must first find where it belongs, then (if it is present) remove it. Since the final "put it there" and "remove it" operations take constant time, all three methods have the same order of running time for a given implementation.

Figure 11-9. Trivial parts of the OrderedList class. The type specified by the type parameter E must be a Comparable type.

1 /** A linked list of Comparable items, in increasing order. */ 2 public class OrderedList<E extends Comparable> 3 implements Set, Predecessor { 4 5 /** The first node in the list. */ 6 private ListNode front; 7 8 /** An OrderedList is initially empty. */ 9 public OrderedList() { 10 front = null; 11 } 12 13 public ListNode getNext() { 14 return front; 15 } 16 17 public void setNext(ListNode next) { 18 front = next; 19 } 20 21 public int size() { 22 int tally = 0; 23 for (ListNode node = front; 24 node != null; 25 node = node.getNext()) { 26 tally++; 27 } 28 return tally; 29 } 30 31 public String toString() { 32 String result = "("; 33 for (ListNode node = front; 34 node != null; 35 node = node.getNext()) { 36 result += node.getItem() + " "; 37 } 38 return result + ")"; 39 } 40 41 }

A comment on terminology: some texts say things like, "An ordered list is a linear-time implementation of the set interface." This is a slight abuse of the terminology, because data structures don't have running times; algorithms do. A more precise statement would be, "In the ordered list implementation of the Set interface, the methods contains(), add(), and remove() all run in linear time."

Search

The contains() method for the OrderedList class (Figure 11-10) is a linear search. As in the linear search of a sorted array (Section 8.1), we can take advantage of the fact that the list elements are in order. If we find an element which is larger than target, we've gone too far and can immediately conclude that target is not in the list.

Figure 11-10. The main loop of the contains() method for the OrderedList class has three branches (lines 511), depending on the result of the comparison.

 1 public boolean contains(E target) {
 2 ListNode node = front;
 3 while (node != null) {
 4 int comparison = target.compareTo(node.getItem());
 5 if (comparison < 0) {
 6 return false;
 7 }
 8 if (comparison == 0) {
 9 return true;
10 }
11 node = node.getNext();
12 }
13 return false;
14 }

As with the linear search algorithm for arrays, this method runs in linear time in the worst case. In an average unsuccessful search, the number of comparisons made is roughly n/2, which is also linear.

Insertion

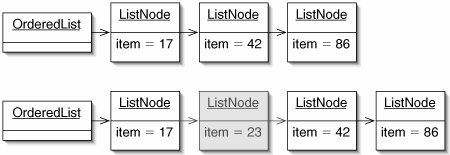
Insertion is slightly more complicated than search. Once we find an item which is larger than target, we have to splice in a new node containing target (Figure 11-11).

Figure 11-11. An OrderedList before (top) and after (bottom) inserting the element 23.

Since splicing in a new node requires knowledge of the previous node, this is a two-finger algorithm (Figure 11-12).

Figure 11-12. With the exception of the emphasized code, add() is identical to contains().

 1 public void add(E target) {
 2 Predecessor prev = this;
 3 ListNode node = front;
 4 while (node != null) {
 5 int comparison = target.compareTo(node.getItem());
 6 if (comparison < 0) {
 7 prev.setNext(new ListNode(target, node));
 8 return;
 9 }
10 if (comparison == 0) {
11 return;
12 }
13 prev = node;
14 node = node.getNext();
15 }
16 prev.setNext(new ListNode(target));
17 }

Deletion

Deletion has the same structure (Figure 11-13), the only difference being that we remove target if we find it and do nothing if we don't.

Figure 11-13. The remove() method.

 1 public void remove(E target) {
 2 Predecessor prev = this;
 3 ListNode node = front;
 4 while (node != null) {
 5 int comparison = target.compareTo(node.getItem());
 6 if (comparison < 0) {
 7 return;
 8 }
 9 if (comparison == 0) {
10 prev.setNext(node.getNext());
11 return;
12 }
13 prev = node;
14 node = node.getNext();
15 }
16 }

The OrderedList data structure is easy to implement, but it requires linear time for search, insertion, and deletion. We will see more efficient data structures in the next two sections. OrderedLists should be used only for very small sets.

Exercises

11.4	In the constructor for the Anagrams class (Figure 11-7, line 14), the add() method is invoked many times on the Set words. If words is an OrderedList, under what circumstances will this take the largest possible amount of time (for a given number of words n)? Is this likely to occur?
11.5	Is it acceptable to swap lines 57 and 810 in Figure 11-10? Explain.

Binary Search Trees