Implementing Stacks and Queues

We now have all the tools we need to implement the Stack and Queue interfaces from Chapter 4.

The ArrayStack Class

The ArrayStack class, which implements the Stack interface, is very similar to Deck. It contains an array data and an int size. When we create a new ArrayStack, data has room for one element and size is 0 (Figure 5-14). The Java wart involving generics and arrays comes up again on line 12. We can't allocate new E[1], so we have to allocate new Object[1] and cast it to E[]. This causes a warning, but there's no way around it.

Figure 5-14. The generic ArrayStack class is similar to Deck.

 1 /** An array-based Stack. */
 2 public class ArrayStack implements Stack {
 3
 4 /** Array of items in this Stack. */
 5 private E[] data;
 6
 7 /** Number of items currently in this Stack. */
 8 private int size;
 9
10 /** The Stack is initially empty. */
11 public ArrayStack() {
12 data = (E[])(new Object[1]); // This causes a compiler warning
13 size = 0;
14 }
15
16 }

The isEmpty() method (Figure 5-15) is identical to the one from Deck.

Figure 5-15. It's easy to determine if an ArrayStack is empty.

1 public boolean isEmpty() {
2 return size == 0;
3 }

The pop() method (Figure 5-16) is similar to deal(), although we throw an exception if the Stack is empty.

Figure 5-16. The pop() method can throw an EmptyStructureException.

1 public Object pop() {
2 if (isEmpty()) {
3 throw new EmptyStructureException();
4 }
5 size--;
6 return data[size];
7 }

The peek() method (Figure 5-17) is even easier because it doesn't change the Stack. We do have to be careful to return the element at position size - 1, which is the top item on the Stack, rather than at position size, which is the next available position in data.

Figure 5-17. The peek() method returns the top element on the Stack.

1 public Object peek() {
2 if (isEmpty()) {
3 throw new EmptyStructureException();
4 }
5 return data[size - 1];
6 }

All that remains is push(). If we try to push something onto a full Stack, the array is stretched, as described in Section 5.1. The code is given in Figure 5-18.

Figure 5-18. The push() method and associated protected methods. The reason for doubling the length of data, rather than merely increasing it by 1, is explained in Chapter 7.

 1 /** Return true if data is full. */
 2 protected boolean isFull() {
 3 return size == data.length;
 4 }
 5
 6 public void push(Object target) {
 7 if (isFull()) {
 8 stretch();
 9 }
10 data[size] = target;
11 size++;
12 }
13

14 /** Double the length of data. */ 15 protected void stretch() { 16 E[] newData = (E[])(new Object[data.length * 2]); // Warning 17 for (int i = 0; i < data.length; i++) { 18 newData[i] = data[i]; 19 } 20 data = newData; 21 }

Figure 5-19 shows the effects of push() and pop() operations on an ArrayStack.

Figure 5-19. Instance diagram showing operations on an ArrayStack. These are the same operations shown in Figure 4-1. The shaded portions of data are not in use.

 

The ArrayQueue Class

The ArrayQueue class, which implements the Queue interface, makes further use of the idea of using only part of an array. There are, of course, complications.

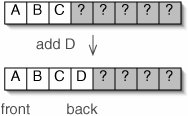
We choose to make higher array indices correspond to elements closer to the back of the Queue. Thus, adding something to an ArrayQueue is exactly like pushing it onto an ArrayStack (Figure 5-20).

Figure 5-20. Adding something into an ArrayQueue is exactly like pushing it onto an ArrayStack. For brevity, we leave out the ArrayStack object and show only the array.

(This item is displayed on page 130 in the print version)

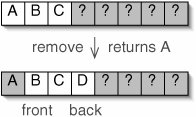
The problem comes when we remove an element from the queue. The first time we do this, the front of the queue is clearly at position 0. Afterward, the front of the queue is at index 1 (Figure 5-21).

Figure 5-21. Removing an element causes the front of the queue to move along the array.

(This item is displayed on page 130 in the print version)

We solve this problem with another field, an int front, which specifies where the queue starts. Whenever we remove, front is incremented, so we know where to find the first element the next time we remove. The next available position for adding is front + size.

There is one more issue. After a series of insertions and deletions, the "in use" portion of the array runs up against the right end of the array. Once this happens, we can't add anything else to the queue, even though there are unused positions.

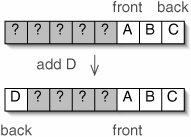
The solution is for the queue to wrap around, so that the next element added goes at position 0. This is illustrated in Figure 5-22.

Figure 5-22. After hitting the right end of the array, the queue wraps around to the beginning.

When we add an element, it should normally be placed at position

front + size

but it should instead be placed at position

front + size - data. length

if the first expression would produce an index beyond the end of the array. We could compute the position with an if statement:

int index = front + size;
if (index >= data.length) {
 index -= data.length;
}

A more elegant solution uses the % operator. Recall that this operator gives the remainder of a division. If we divide front + size by the capacity of the queue, the quotient is either 0 or 1. If it is 0, the % operator has no effect. If it is 1, the % operator subtracts the capacity one time. The single expression

(front + size) % data.length

therefore always produces the right index.

The code for the ArrayQueue class is given in Figure 5-23.

Figure 5-23. The ArrayQueue class.

1 /** An array-based Queue. */ 2 public class ArrayQueue implements Queue { 3 4 /** Array of items in this Queue. */ 5 private E[] data; 6 7 /** Index of the frontmost element in this Queue. */ 8 private int front; 9 10 /** Number of items currently in this Queue. */ 11 private int size; 12 13 /** The Queue is initially empty. */ 14 public ArrayQueue() { 15 data = (E[])(new Object[1]); // This causes a compiler warning 16 size = 0; 17 front = 0; 18 } 19 20 public void add(E target) { 21 if (isFull()) { 22 stretch(); 23 } 24 data[(front + size) % data.length] = target; 25 size++; 26 } 27 28 public boolean isEmpty () { 29 return size == 0; 30 } 31 32 /** Return true if data is full. */ 33 protected boolean isFull() { 34 return size == data.length; 35 } 36 37 public E remove() { 38 if (isEmpty()) { 39 throw new EmptyStructureException(); 40 } 41 E result = data[front]; 42 front = (front + 1) % data.length; 43 size--; 44 return result; 45 } 46 47 /** Double the length of data. */ 48 protected void stretch() { 49 E[] newData = (E[])(new Object[data.length * 2]); // Warning 50 for (int i = 0; i < data.length; i++) { 51 newData[i] = data[(front + i) % data.length]; 52 } 53 data = newData; 54 front = 0; 55 } 56 57 }

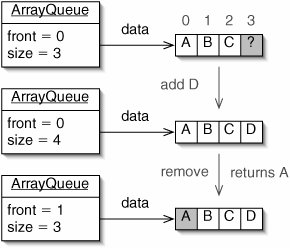
The operation of an ArrayQueue is illustrated in Figure 5-24.

Figure 5-24. Operations on an ArrayQueue. These are the same operations shown in Figure 4-29.

Exercises

5.7	Suppose we modified line 12 of Figure 5-14 so that, in a new ArrayStack, data was an array of length 0. What problem would this cause?
5.8	Show that, when playing Idiot's Delight, there will never be more than 13 cards in any one stack. We can avoid stretching the stacks if we allocate an array this large when each ArrayStack is first constructed. Write a second, overloaded constructor for the ArrayStack class which takes one argument capacity and initializes data to be an array of length capacity. Modify the IdiotsDelight class to take advantage of this new constructor.
5.9	Can Deck be written as a subclass of ArrayStack? If so, is it a good idea? If not, why not?
5.10	Draw an instance diagram of an ArrayStack as it would look if, immediately after pushing D in Figure 5-19, we pushed E.
5.11	Write a toString() method for the ArrayStack class. Discuss whether it is preferable for the top of the Stack to appear on the left or the right end of the returned String.
5.12	What would happen if we were to add something to a full ArrayQueue without stretching the array?
5.13	Why is the stretch() method from ArrayQueue (Figure 5-23) more complicated than the one from ArrayStack (Figure 5-18)?
5.14	Write a toString() method for the ArrayQueue class. Discuss whether it is preferable for the front of the queue to appear on the left or the right end of the returned String.