Shrinking and Stretching Arrays
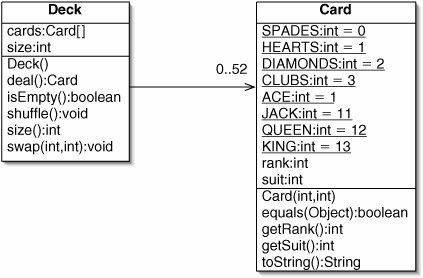
The size of an array is determined when it is allocated. We can overwrite individual elements, but we can't make the array longer or shorter. In this section, we will see some ways around this problem. As a running example, we will write the Deck class, which we mentioned in Chapter 4. A Deck holds a varying number of Cardsoriginally 52, fewer as Cards are dealt from the Deck. These two classes are illustrated in Figure 5-1.
Figure 5-1. UML class diagram of the Deck and Card classes.
The Card Class
Before writing Deck, let's take a moment to write Card. A Card has two fields, rank and suit. Since, once a Card is created, these things never change, we don't provide mutators for them, only accessors (Figure 5-2).
Figure 5-2. Fields, constructor, and accessors for the Card class.
1 /** A playing card. */
2 public class Card {
3
4 /** Number or face on this Card. */
5 private int rank;
6
7 /** Suit of this Card. */
8 private int suit;
9
10 /** Initialize the rank and suit. */
11 public Card(int rank, int suit) {
12 this.rank = rank;
13 this.suit = suit;
14 }
15
16 /** Return the rank of this Card. */ 17 public int getRank() { 18 return rank; 19 } 20 21 /** Return the suit of this Card. */ 22 public int getSuit() { 23 return suit; 24 } 25 26 } |
The rank is either a number or one of ace, jack, king, or queen. We assign the values 1, 11, 12, and 13, respectively, to these other values. Rather than have these magic numbers scattered all over our code, we define a constant for each one. Similarly, we define a constant for each suit (Figure 5-3).
Figure 5-3. Constants from the Card class.
1 /** Suit of spades. */ 2 public static final int SPADES = 0; 3 4 /** Suit of hearts. */ 5 public static final int HEARTS = 1; 6 7 /** Suit of diamonds. */ 8 public static final int DIAMONDS = 2; 9 10 /** Suit of clubs. */ 11 public static final int CLUBS = 3; 12 13 /** Rank of ace, equivalent to 1. */ 14 public static final int ACE = 1; 15 16 /** Rank of jack. */ 17 public static final int JACK = 11; 18 19 /** Rank of queen. */ 20 public static final int QUEEN = 12; 21 22 /** Rank of king. */ 23 public static final int KING = 13; |
All that remain are the standard methods equals() and toString() (Figure 5-4). Note that suit is ignored in equals(). The charAt() method from the String class is used to good effect in the toString() method.
Figure 5-4. Remaining methods from the Card class. An extra character is included at the beginning of the String of rank names because 'A' corresponds to 1, not 0.
1 /**
2 * Return true if and only if that Card has the same rank as
3 * this one. Suit is ignored.
4 */
5 public boolean equals(Object that) {
6 if (this == that) {
7 return true;
8 }
9 if (that == null) {
10 return false;
11 }
12 if (getClass() != that.getClass()) {
13 return false;
14 }
15 Card thatCard = (Card)that;
16 return rank == thatCard.rank;
17 }
18
19 public String toString() {
20 return "" + "-A23456789TJQK".charAt(rank) + "shdc".charAt(suit);
21 }
|
Shrinking Arrays
It is clear that the Deck class will need an array of Cards. Specifically, since a Deck can never hold more than 52 cards, this array should have a length of 52 (Figure 5-5).
Figure 5-5. A first draft of the Deck class. The constructor does not yet create the Cards as the comment promises.
1 /** Standard deck of 52 playing cards. */
2 public class Deck {
3
4 /** The Cards in this Deck. */
5 private Card[] cards;
6
7 /** Create all 52 Cards, in order. */
8 public Deck() {
9 cards = new Card[52];
10 }
11
12 }
|
When we create an instance of this class, we have room for 52 cards (Figure 5-6). The problem, of course, is that we don't always need this much room. How can we change the size of the array?
Figure 5-6. A Deck contains an array of Cards. The array has length 52.

The secret is to include an extra field in Deck: an int size telling us how many Cards are currently in the Deck. Only the first size elements in the array are considered part of the Deck. For example, if size is 3, then only elements 0, 1, and 2 are considered part of the Deck. While elements 3 and later have values, we don't know or care what they are. This is shown in Figure 5-7.
Figure 5-7. The field size indicates that only the first three positions in the array cards are considered "in use." This figure shows two instance diagrams of the same structure. The version above makes it explicit that each of the first three elements of cards is a reference to a Card instance. The version below simply shows each Card's rank and suit in the corresponding array position.

It is important to distinguish between the size of the Deck (how many Cards it currently contains) and the capacity of the Deck (the maximum number of Cards it can contain52).
With this idea in mind, we can rewrite the Deck class so that the constructor fills the Deck with 52 Cards (Figure 5-8). This version of the constructor also creates all of the Cards by looping through the suits and the ranks.
The field size makes certain methods extremely easy to write (Figure 5-9).
Figure 5-8. By the end of the constructor for the revised Deck class, size is 52.
1 /** Standard deck of 52 playing cards. */
2 public class Deck {
3
4 /** The Cards in this Deck. */
5 private Card[] cards;
6
7 /** Number of Cards currently in this Deck. */
8 private int size;
9
10 /** Create all 52 Cards, in order. */
11 public Deck() {
12 cards = new Card[52];
13 size = 0;
14 for (int suit = Card.SPADES; suit <= Card.CLUBS; suit++) {
15 for (int rank = Card.ACE; rank <= Card.KING; rank++) {
16 cards[size] = new Card(rank, suit);
17 size += 1;
18 }
19 }
20 }
21
22 }
|
Figure 5-9. Methods indicating the fullness of a Deck are trivial.
1 /** Return true if the Deck contains no Cards. */
2 public boolean isEmpty() {
3 return size == 0;
4 }
5
6 /** Return the number of Cards currently in the Deck. */
7 public int size() {
8 return size;
9 }
|
The only method (besides the constructor) that modifies size is deal(), which removes and returns the top card on the Deck (Figure 5-10).
Figure 5-10. The deal() method modifies the field size.
1 /** Remove one Card from the Deck and return it. */
2 public Card deal() {
3 size--;
4 return cards[size];
5 }
|
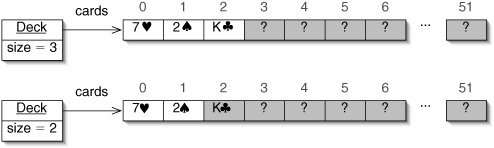
Although deal() is a very short method, its behavior is interesting. It begins by reducing the size of the Deck on line 3. The Card we want to return is now at index size. This is in the "not in use" part of the Deck, but the Card is still there, so we can return it in line 4. This is illustrated in Figure 5-11.
Figure 5-11. Dealing from a Deck. The Deck before dealing, with the king of clubs on top, is shown above. When size is reduced (below), element 2 ceases to be part of the Deck, but the value at that position does not change, so we can still return it.
All that remains to complete the Deck class is the shuffle() method. This could get quite complicated if we attempted to model the "riffle shuffle" that most Americans use when shuffling physical cards. Fortunately, there is a simpler algorithm. We must separate the problem specification (rearrange the Cards in a random order) from the algorithm we happen to know.
Rearranging the Cards in a random order means that any Card is equally likely to end up in position 51, any of the remaining Cards is equally likely to end up in position 50, and so on down. A simple algorithm falls out of this definition. We pick one index at random and swap the Card at that position with the one at position 51. There is a small probability (1 in 52) that we will pick index 51, but this is not a problem: we just swap the Card at position 51 with itself, which has no effect. There is a 1 in 52 chance that the Card that was on top of the Deck will remain there, which is exactly what we want.
We then pick one of the 51 remaining indices (0 through 50) and swap the Card there with the one at position 50. This continues down through position 1. We don't have to choose a random Card to swap into position 0, because there's only one Card left to choose from at that point.
The shuffle() method is shown in Figure 5-12. The swapping of Cards is handled by the method swap(). Since we don't want users of the Deck class to be swapping Cards at arbitrary indices (especially indices which are greater than or equal to size), we declare swap() protected.
Stretching Arrays
The field size allows us to change the size of a Deck at will, as long as size never exceeds the actual length of the array. What if a structure needs to grow beyond its original capacity? While this isn't necessary in a Deck, it is certainly an issue for stacks and queues, which can become arbitrarily large.
Figure 5-12. The methods shuffle() and swap().
1 /** Randomly rearrange the Cards in the Deck. */
2 public void shuffle() {
3 for (int i = size - 1; i > 0; i--) {
4 swap(i, (int)(Math.random() * (i + 1)));
5 }
6 }
7
8 /** Swap the Cards at indices i and j. */
9 protected void swap(int i, int j) {
10 Card temp = cards[i];
11 cards[i] = cards[j];
12 cards[j] = temp;
13 }
|
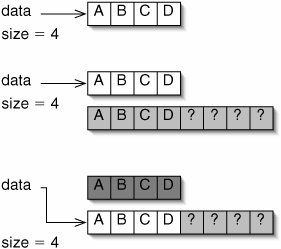
The solution to this problem is somewhat shocking: we copy the entire contents of the array into a new, larger array (Figure 5-13). This operation can be time consuming, although we will see in Chapter 7 that it is not quite as bad as it appears.
Figure 5-13. Stretching an array. The array data is full (top), so we can't add more elements. Instead, we copy the elements into a new, larger array (middle). Finally, data becomes a reference to the new array (bottom).
Exercises
| 5.1 |
Explain how to modify the Card class so that aces rank above kings, rather than below twos. |
| 5.2 |
What would be the effect of swapping lines 14 and 15 in Figure 5-8? |
| 5.3 |
Modify the deal() method (Figure 5-10) so that it throws an EmptyStructureException (Figure 4-27) if the Deck is empty. |
| 5.4 |
Is it okay to invoke shuffle() on a non-full Deck? Explain. |
| 5.5 |
Write a main() method to test the Deck class. |
| 5.6 |
Does the stretching operation shown in Figure 5-13 alter the data structure's size or its capacity? |
Part I: Object-Oriented Programming
Encapsulation
Polymorphism
Inheritance
- Inheritance
- Extending a Class
- The Object Class
- Packages and Access Levels
- Summary
- Vocabulary
- Problems
- Projects
Part II: Linear Structures
Stacks and Queues
- Stacks and Queues
- The Stack Interface
- The Call Stack
- Exceptions
- The Queue Interface
- Summary
- Vocabulary
- Problems
- Projects
Array-Based Structures
- Array-Based Structures
- Shrinking and Stretching Arrays
- Implementing Stacks and Queues
- The List Interface
- Iterators
- The Java Collections Framework: A First Look
- Summary
- Vocabulary
- Problems
- Projects
Linked Structures
- Linked Structures
- List Nodes
- Stacks and Queues
- The LinkedList Class
- The Java Collections Framework Revisited
- Summary
- Vocabulary
- Problems
- Projects
Part III: Algorithms
Analysis of Algorithms
- Analysis of Algorithms
- Timing
- Asymptotic Notation
- Counting Steps
- Best, Worst, and Average Case
- Amortized Analysis
- Summary
- Vocabulary
- Problems
- Projects
Searching and Sorting
- Searching and Sorting
- Linear Search
- Binary Search
- Insertion Sort
- The Comparable Interface
- Sorting Linked Lists
- Summary
- Vocabulary
- Problems
- Projects
Recursion
- Recursion
- Thinking Recursively
- Analyzing Recursive Algorithms
- Merge Sort
- Quicksort
- Avoiding Recursion
- Summary
- Vocabulary
- Problems
- Projects
Part IV: Trees and Sets
Trees
Sets
- Sets
- The Set Interface
- Ordered Lists
- Binary Search Trees
- Hash Tables
- The Java Collections Framework Again
- Summary
- Vocabulary
- Problems
- Projects
Part V: Advanced Topics
Advanced Linear Structures
- Advanced Linear Structures
- Bit Vectors
- Sparse Arrays
- Contiguous Representation of Multidimensional Arrays
- Advanced Searching and Sorting
- Summary
- Vocabulary
- Problems
- Projects
Strings
Advanced Trees
- Advanced Trees
- Heaps
- Disjoint Set Clusters
- Digital Search Trees
- Red-Black Trees
- Summary
- Vocabulary
- Problems
- Projects
Graphs
- Graphs
- Terminology
- Representation
- Graph Traversal
- Topological Sorting
- Shortest Paths
- Minimum Spanning Trees
- Summary
- Vocabulary
- Problems
- Projects
Memory Management
Out to the Disk
- Out to the Disk
- Interacting with Files
- Compression
- External Sorting
- B-Trees
- Summary
- Vocabulary
- Problems
- Projects
Part VI: Appendices
A. Review of Java
- A. Review of Java
- A.1. The First Program
- A.2. Variables and Types
- A.3. Loops
- A.4. Interacting with the User
- A.5. Branching
- A.6. Methods and Breaking Out
- A.7. Constants
- A.8. Operators
- A.9. Debugging
- A.10. Coding Conventions
B. Unified Modeling Language
C. Summation Formulae
- C. Summation Formulae
- C.1. Sum Notation
- C.2. Sum of Constants
- C.3. Sum of First n Integers
- C.4. Sums of Halves and Doubles
- C.5. Upper Limit on Sum of a Function
- C.6. Constant Factors
D. Further Reading
Index
EAN: 2147483647
Pages: 216
- The Second Wave ERP Market: An Australian Viewpoint
- The Effects of an Enterprise Resource Planning System (ERP) Implementation on Job Characteristics – A Study using the Hackman and Oldham Job Characteristics Model
- Data Mining for Business Process Reengineering
- Intrinsic and Contextual Data Quality: The Effect of Media and Personal Involvement
- Healthcare Information: From Administrative to Practice Databases
