Counting Steps

Now we know what we're aiming for when we analyze an algorithm: the order of the running time. We accomplish this through the following process:

1. Write the algorithm down in precise English or in any programming language, such as Java.
2. Determine how many steps are accomplished by each line and how many times the line is executed. The time used by the line is the product of these two expressions. We'll say more in a moment about what constitutes a step.
3. The total running time for the algorithm is the sum of the time required for each line. The order of this expression is the same as the order of the most time-consuming line.

For example, let's analyze the size() method from our LinkedList class. The method is reproduced in Figure 7-10, with extra line breaks added to keep each line simple. The time this takes depends on the size of the list, which we'll call n.

Each line here performs only a single step. We define a step as a constant amount of work. In other words, a step cannot depend on the size of the input or data structure in question. Any of the following constitutes a single step:

• Accessing or setting a variable or field, including an element of an array.
• Addition, subtraction, multiplication, division, and other basic arithmetic operators. (Strictly speaking, the time it takes to add two numbers depends on the sizes of the numbers. Since numbers in Java, as in most other programming languages, have a limited range, there is no potential for abuse by adding thousand-digit numbers.)
• Finding the length of an array or String.

Figure 7-10. The size() method from our LinkedList class. The three parts of the for loop header have been placed on separate lines for clarity.

1 public int size() {
2 int tally = 0;
3 for (ListNode node = front;
4 node != null;
5 node = node.getNext()) {
6 tally++;
7 }
8 return tally;
9 }

• Comparisons using ==, <, etc.
• Any fixed number of single steps, such as two additions and a variable assignment.

All of the operators which are built into the Java language, such as + and &&, count as single steps. This is not necessarily true of methods in the Java library, such as those in the collections framework. In general, if a method or operation is so trivial that you cannot imagine what simpler operations might be used to construct it, it can probably be considered a single step.

It is not a problem that some steps take longer than others, since they are all in Q(1). Suppose the longest step takes 100 milliseconds and the shortest step takes 20 milliseconds. Assuming that every step takes 100 milliseconds gives us an upper bound on the total running time. Assuming that every step takes 20 milliseconds gives us a lower bound. These two running-time expressions are in the same order, so they are equivalent for our purposes.

Returning to size(), we see that each line performs a single step, except for lines 7 and 9, which don't do anything. How many times is each line executed?

Lines 1, 2, 3, and 8 are executed only once. The for loop test on line 4 is executed once each time we enter the loop, plus one more time when the test fails. Lines 5 and 6 are each executed once on each pass through the loop.

Since tally starts at 0 and ends up equal to n, there must be n passes through the loop. We now know how much total time is taken by each line, as summarized in Figure 7-11. Line 4 does the most work, taking total time in Q(n + 1) = Q(n). We conclude that the running time for size() is linear.

Alternately, let c be the time taken by a single step. The total time taken by size() is:

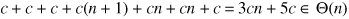
Most algorithms are analyzed in terms of n, with n being the size of some data structure. Other analyses are possible. For example, the constructor for the Deck class from Chapter 5 is shown in Figure 7-12. This is analyzed in terms of r, the number of ranks, and s, the number of suits. The running time is dominated by line 9, which takes time in Q((r + 1)s) = Q(rs).

It is not always possible to write an algorithm so that each line takes only one step each time it is run. For example, suppose we want to analyze the contructor for the GoFish class, again in terms of r and s. The constructor is reproduced in Figure 7-13. Line 5 invokes the Deck constructor, which uses more than one step. Even though it is executed only once, this turns out to be the most expensive line in the algorithm. The analysis of shuffle() is left as Exercise 7.10. It is not precisely true that the add() method invoked in lines 12 and 13 takes constant time, but this can be remedied by a simple modification (Exercise 7.11).

Figure 7-11. The size() method, with the time taken by each line.

1 public int size() { // 1 step, once
2 int tally = 0; // 1 step, once
3 for (ListNode node = front; // 1 step, once
4 node != null; // 1 step, n + 1 times
5 node = node.getNext()) { // 1 step, n times
6 tally++; // 1 step, n times
7 }
8 return tally; // 1 step, once
9 }

Figure 7-12. The constructor for the Deck class can be analyzed in terms of s, the number of suits, and r, the number of ranks.

 1 /** Create all 52 Cards, in order. */
 2 public Deck() { // 1 step, once
 3 cards = new Card[52]; // 1 step, once
 4 size = 0; // 1 step, once
 5 for (int suit = Card.SPADES; // 1 step, once
 6 suit <= Card.CLUBS; // 1 step, s + 1 times
 7 suit++) { // 1 step, s times
 8 for (int rank = Card.ACE; // 1 step, s times
 9 rank <= Card.KING; // 1 step, (r + 1)s times
10 rank++) { // 1 step, rs times
11 cards[size] = new Card(rank, suit); // 1 step, rs times
12 size += 1; // 1 step, rs times
13 }
14 }
15 }

Since we can ignore all lines except the one with the highest-order running time, it is often okay to collapse several lines together. Specifically, all three parts of a for loop header can be taken as a single step, which is run as many times as the loop testthat is, one more than the number of passes through the loop. An example, a method to add up the elements of a two-dimensional array (matrix), is given in Figure 7-14.

A trickier algorithm to analyze is one which adds up only the numbers for which j 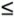The dominant term in the running time of this algorithm is the number of times the inner loop (lines 79) runs. This number is not immediately obvious, because it is different in each pass through the outer loop. When i is 0, the inner loop runs once. When i is 1, the inner loop runs twice. This continues until i is n 1, when the inner loop runs n times. The total number of passes through the inner loop, then, is:

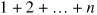
This can be rewritten as:

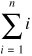
Figure 7-13. Some lines in the constructor from the GoFish class take more than one step.

 1 /** Shuffle the Deck and deal seven Cards to each player. */
 2 public GoFish() { // 1 step, once
 3 computerScore = 0; // 1 step, once
 4 playerScore = 0; // 1 step, once
 5 deck = new Deck(); // (r + 1)s steps, once
 6 deck.shuffle(); // rs + 1 steps, once
 7 computerHand = new GoFishHand(); // 1 step, once
 8 playerHand = new GoFishHand(); // 1 step, once
 9 for (int i = 0; // 1 step, once
10 i < 7; // 1 step, 8 times
11 i++) { // 1 step, 7 times
12 playerHand.add(deck.deal()); // 1 step, 7 times
13 computerHand.add(deck.deal()); // 1 step, 7 times
14 }
15 }

Figure 7-14. This method accepts an n x n array as input and runs in Q(n2) time. Each line counts as a single step, so only the number of times each line is executed is shown.

 1 /** Return the sum of the elements of matrix. */
 2 public static double sum(double[][] matrix) { // once
 3 double result = 0; // once
 4 for (int i = 0; i < matrix.length; i++) { // n + 1 times
 5 for (int j = 0; j < matrix[i].length; j++) { // n(n + 1) times
 6 result += matrix[i][j]; // n * n times
 7 }
 8 }
 9 return result; // once
10 }

Figure 7-15. In this method, the number of times the inner loop runs depends on the value of i.

 1 /**
 2 * Return sum of matrix elements on or below the diagonal.
 3 */
 4 public static double sumLowerTriangle(double[][] matrix) {
 5 double result = 0;
 6 for (int i = 0; i < matrix.length; i++) {
 7 for (int j = 0; j <= i; j++) {
 8 result += matrix[i][j];
 9 }
10 }
11 return result;
12 }

Using the theorem from Section C.3 of Appendix C, we determine that this is:

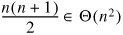
A slightly easier approach is to reason that, on each pass through the outer loop, the inner loop runs at most n times. Using the theorem from Section C.5, we have:

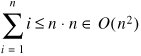
Because of the 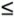, this allows us to make only a O statement, not a Q(n), while a doubly nested for loop typically takes time in Q(n2). Figure 7-16 shows a method with a quadruply nested for loop.

It is very easy to find an asymptotic upper bound on the running time of sum4d(). The first loop, starting on line 4, runs n times. The second loop runs at most n times for each pass through the first loop, for a total in O(n2). Similarly, the third loop takes time in O(n3). The fourth loop (and hence the entire method) takes time in O(n4).

We must be careful not to overgeneralize the result about nested loops. It is safe to use only for loops of the common form

for (int i = 0; i < n; i++) {
 ...
}

which run at most n times.

Figure 7-16. This method, which sums the elements of a four-dimensional array, contains a quadruply nested for loop.

 1 /** Return the sum of the elements of arr. */
 2 public static double sum4d(double[][][][] arr) { // once
 3 double result = 0; // once
 4 for (int i = 0; i < arr.length; i++) { // O(n) times
 5 for (int j = 0; j < i; j++) { // O(n2) times
 6 for (int k = 0; k < j; k++) { // O(n3) times
 7 for (int m = 0; m < k; m++) { // O(n4) times
 8 result += arr[i][j][k][m]; // O(n4) times
 9 }
10 }
11 }
12 }
13 return result; // once
14 }

An enhanced for loop also runs at most n times, where n is the number of elements in the data structure being traversed.

A loop may run less than n times if it is stopped early by a return or break statement, or if it deals with more than one element on each pass.

Exercises

7.9	An instance of the built-in class java.lang.BigInteger represents an integer, which can be arbitrarily large. Is it safe to assume that the add() method from this class takes constant time? Explain.
7.10	Analyze the running time of the shuffle() method from the Deck class (Figure 5-12) in terms of r and s.
7.11	Modify the Go Fish program so that the add() method of the GoFishHand class takes constant time. (Hint: See Exercise 5.8.)
7.12	Show that the running time of sum4d() (Figure 7-16) is in Q(n4).

Best, Worst, and Average Case