Terminology

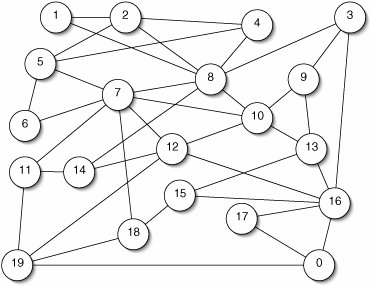
Understanding graphs allows us to create much more elaborate games than we could before. Almost any game board can be treated as a graph. For a concrete example, we present the game of Galaxy (Figure 15-2).

Galaxy

Players: 2

Object: To score the most points.

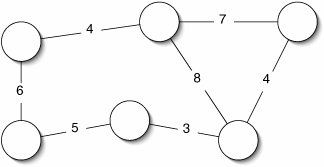
Board: There are twenty stars in the galaxy, connected by lines as shown below. Each player initially controls one star chosen at random.

Play: On a turn, choose any unoccupied star and occupy it. Score a point for each adjacent enemy star.

Game End: The game ends when all 20 stars are occupied.

A partial transcript using our implementation is given in Figure 15-3.

Figure 15-3. Sample move in a game of Galaxy. Player 2 scores 2 points occupying star 4, which is adjacent to two stars occupied by player 1: star 5 and star 8.

(This item is displayed on pages 409 - 410 in the print version)

 1 Star Owner Neighbors
 2 0 0 [ 16 17 19 ]
 3 1 0 [ 2 8 ]
 4 2 0 [ 1 4 5 8 ]
 5 3 0 [ 8 9 16 ]
 6 4 0 [ 2 5 8 ]
 7 5 1 [ 2 4 6 7 ]

8 6 0 [ 5 7 ] 9 7 2 [ 5 6 8 10 11 12 18 ] 10 8 1 [ 1 2 3 4 7 10 14 ] 11 9 0 [ 3 10 13 ] 12 10 1 [ 7 8 9 12 13 ] 13 11 0 [ 7 14 19 ] 14 12 2 [ 7 10 14 16 19 ] 15 13 0 [ 9 10 15 16 ] 16 14 0 [ 8 11 12 ] 17 15 0 [ 13 16 18 ] 18 16 0 [ 0 3 12 13 15 17 ] 19 17 0 [ 0 16 ] 20 18 0 [ 7 15 19 ] 21 19 0 [ 0 11 12 18 ] 22 Player 1: 2 23 Player 2: 2 24 25 Player 2, pick a star: 4 26 Star Owner Neighbors 27 0 0 [ 16 17 19 ] 28 1 0 [ 2 8 ] 29 2 0 [ 1 4 5 8 ] 30 3 0 [ 8 9 16 ] 31 4 2 [ 2 5 8 ] 32 5 1 [ 2 4 6 7 ] 33 6 0 [ 5 7 ] 34 7 2 [ 5 6 8 10 11 12 18 ] 35 8 1 [ 1 2 3 4 7 10 14 ] 36 9 0 [ 3 10 13 ] 37 10 1 [ 7 8 9 12 13 ] 38 11 0 [ 7 14 19 ] 39 12 2 [ 7 10 14 16 19 ] 40 13 0 [ 9 10 15 16 ] 41 14 0 [ 8 11 12 ] 42 15 0 [ 13 16 18 ] 43 16 0 [ 0 3 12 13 15 17 ] 44 17 0 [ 0 16 ] 45 18 0 [ 7 15 19 ] 46 19 0 [ 0 11 12 18 ] 47 Player 1: 2 48 Player 2: 4

This user interface clearly leaves something to be desired; improving it is left as Problem 15.28.

Before writing the code for Galaxy, we introduce some graph terminology.

A graph consists of vertices (nodes) and edges. In a drawing, the vertices are shown as circles and the edges are shown as lines or arrows.

In an directed graph, an edge is an arrow going from one vertex to another (Figure 15-4). In some situations, it is meaningful to have a self-loop, an edge connecting a vertex to itself. In an undirected graph, an edge is simply a line connecting two vertices. Undirected graphs usually do not have self-loops. For every undirected graph there is a corresponding directed graph where each undirected edge is replaced by two directed edges, one in each direction.

Figure 15-4. Directed (left) and undirected (right) graphs. Vertex G in the directed graph has a self-loop.

(This item is displayed on page 411 in the print version)

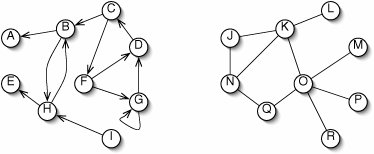
The neighbors of a vertex are those vertices that can be reached by moving along one edge. In Figure 15-4, the neighbors of N are J, K, and Q. The neighbors of H are E and B, but not Iit is illegal to move backward along a directed edge.

A path from one vertex to another is a sequence of vertices, each a neighbor of the previous one. In Figure 15-4, the sequence IHimages/U2192.jpg border=0>Bimages/U2192.jpg border=0>A is a path from I to A. The distance between two vertices is the length of the shortest path between them.

A cycle is a path (of length one or more) from a vertex back to itself. In Figure 15-4, Fimages/U2192.jpg border=0>Gimages/U2192.jpg border=0>Dimages/U2192.jpg border=0>Cimages/U2192.jpg border=0>F is a cycle. In an undirected graph, a cycle may not follow the same edge more than once. Thus, Jimages/U2192.jpg border=0>Kimages/U2192.jpg border=0>Nimages/U2192.jpg border=0>J is a cyle, but not Qimages/U2192.jpg border=0>Nimages/U2192.jpg border=0>Q.

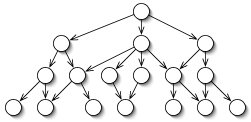
A graph with no cycles is called acyclic. A directed acyclic graph is sometimes called a dag (Figure 15-5).

Figure 15-5. A directed acyclic graph or dag.

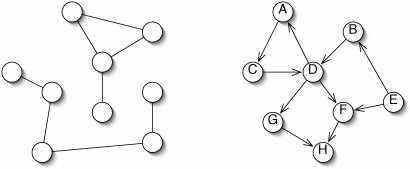
A graph in which every pair of vertices is connected by a path (not necessarily an edge) is said to be connected (Figure 15-6). Not all graphs are connected.

Figure 15-6. The undirected graph at left is not connected. The directed graph at right appears to be connected, but it is not: there is, for example, no path from F to E.

Data are usually associated only with the vertices of a graph. Occasionally, there are also data (usually numbers) associated with the edges (Figure 15-7). Such a number might represent the length of a road between two cities or the price of a cable between two computers. Such graphs are called weighted graphs.

Figure 15-7. In a weighted graph, there are data associated with the edges.

When analyzing graph algorithms, we often give results in terms of v (the number of vertices) and e (the number of edges). In a directed graph, each of the v vertices might have an edge leading to itself and every other vertex, so e

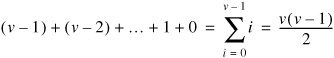
In either case e O(dense. A graph with far fewer edges is called sparse.

Exercises

15.1	Is the graph for the Galaxy game (Figure 15-2) directed or undirected? Weighted or unweighted? Connected or unconnected?
15.2	Which vertex in the graph for the Galaxy game has the most neighbors?
15.3	Find a cycle of length 6 in the graph for the Galaxy game (Figure 15-2).
15.4	Is a dag always, sometimes, or never connected?
15.5	What is the maximum number of edges in a directed graph with no self-loops?
15.6	What is the minimum length of a cycle in an undirected graph?
15.7	What is the minimum number of edges in a connected, undirected graph?
15.8	What is the minimum number of edges in a connected, directed graph?