Binary Search Trees

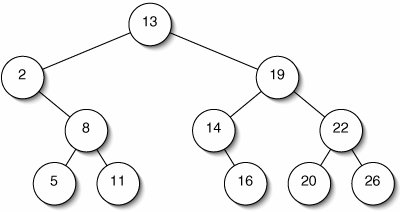
We now turn to a second implementation of the Set interface, which is more efficient under some circumstances. A binary search tree is a binary tree in which all of the items in the left subtree are less than the root and all of the items in the right subtree are greater than the root. The subtrees are themselves binary search trees. An example is shown in Figure 11-14.

Figure 11-14. In a binary search tree, numbers less than the root are in the left subtree, while numbers greater than the root are in the right subtree. The subtrees are themselves binary search trees.

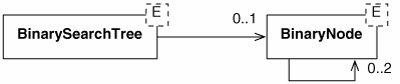
We use the linked representation of binary trees from Section 10.1. Like an instance of the Questions class from Chapter 10, a (non-empty) BinarySearchTree object contains (a reference to) a BinaryNode (Figure 11-15). This may in turn contain additional BinaryNodesthe roots of its subtrees.

Figure 11-15. A BinarySearchTree instance usually contains a BinaryNode, which can contain further BinaryNodes.

(This item is displayed on page 297 in the print version)

The easy parts of the BinarySearchTree class are given in Figure 11-16. Like the OrderedList class, this is suitable only for Sets of Comparable objects.

Figure 11-16. Easy parts of the BinarySearchTree class. Like many tree-related methods, the size() method is recursive.

 1 /** A binary search tree of Comparables. */
 2 public class BinarySearchTree>
 3 implements Set {
 4
 5 /** Root node. */
 6 private BinaryNode root;
 7
 8 /** A BinarySearchTree is initially empty. */
 9 public BinarySearchTree() {
10 root = null;
11 }
12
13 public int size() {
14 return size(root);
15 }
16
17 /** Return the size of the subtree rooted at node. */
18 protected int size(BinaryNode node) {
19 if (node == null) {
20 return 0;
21 } else {
22 return 1 + size(node.getLeft()) + size(node.getRight());
23 }
24 }
25
26 }

Search

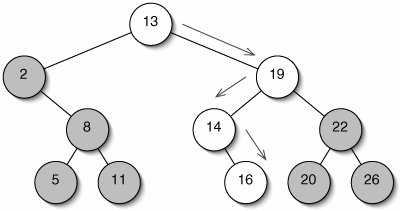
The advantage of a binary search tree is that we may have to look at very few of the items in the tree to determine whether some target is present (Figure 11-17). We start by comparing the target to the root. Depending on the result of this comparison, we either descend to the left child, declare success, or descend to the right child. The search fails only if we try to descend to a nonexistent childfor example, we try to go right when there is no right child.

Figure 11-17. Successful search for 16 in a binary search tree. The shaded nodes are never examined.

The code for the contains() method (Figure 11-18) is similar to the version from the OrderedList class. As we examine each node, we decide what to do next based on the result of comparing target with the item in the current node.

Figure 11-18. On each pass through the main loop, the contains() method checks whether target is less than, equal to, or greater than the item in node.

 1 public boolean contains(E target) {
 2 BinaryNode node = root;
 3 while (node != null) {
 4 int comparison = target.compareTo(node.getItem());
 5 if (comparison < 0) { // Go left
 6 node = node.getLeft();
 7 } else if (comparison == 0) { // Found it
 8 return true;
 9 } else { // Go right
10 node = node.getRight();
11 }
12 }
13 return false;
14 }

Searching a binary search tree is often much faster than searching an ordered list, because the number of comparisons we have to make is not proportional to the number of nodes in the tree, but merely to the height of the tree. In a perfect tree, this is Q(log n).

Unfortunately, binary search trees are generally not perfect. In the worst case, each internal node has only one child. This happens in the Anagrams program when the word file is in alphabetical order: every new node is a right child. When this happens, search takes linear time.

While the analysis is beyond the scope of this book, it turns out that on average (assuming items are inserted in random order and there are no deletions), the running times of contains(), add(), and remove() for binary search trees are all in Q(log n).

Insertion

When we insert something into a binary search tree, we must first search for it. We have to make a change only if the search fails. This means that we have just tried to descend into a null child. All we have to do is add a new leaf node at that position (Figure 11-19).

Figure 11-19. Inserting 15 into a binary search tree. The search fails when 16 has no left child, so we add a new leaf there.

There are two complications to the code:

• Once we reach a null node, we have forgotten how we got there. Since we need to modify either the left or right field in the parent of the new leaf, we'll need this information.
• We need to deal with the situation in which the binary search tree is empty.

These are the same problems we had when adding an element to the end of a LinkedList (Section 6.3). The solution is also the same. We define an interface Parent (Figure 11-20), which is implemented by both the BinaryNode and BinarySearchTree classes. Where the Predecessor interface had a setNext() method, the Parent interface has a setChild() method. The first argument to setChild() is an int specifying which child to set. The comment defines the meaning of this int in such a way that we can use the result of an invocation of compareTo() to determine which child to set.

The implementations of these methods for the BinaryNode class are trivial (Figure 11-21).

Figure 11-20. Both the BinaryNode and BinarySearchTree classes must be modified to implement the Parent interface.

 1 /**
 2 * Something which has children, such as a BinarySearchTree or a
 3 * BinaryNode.
 4 */
 5 public interface Parent {
 6
 7 /**
 8 * Return the left child if direction < 0, or the right child
 9 * otherwise.
10 */
11 public BinaryNode getChild(int direction);
12
13 /**
14 * Replace the specified child of this parent with the new child.
15 * If direction < 0, replace the left child. Otherwise, replace
16 * the right child.
17 */
18 public void setChild(int direction, BinaryNode child);
19
20 }

Figure 11-21. The getChild() and setChild() methods for the BinaryNode class.

 1 public BinaryNode getChild(int direction) {
 2 if (direction < 0) {
 3 return left;
 4 } else {
 5 return right;
 6 }
 7 }
 8
 9 public void setChild(int direction, BinaryNode child) {
10 if (direction < 0) {
11 left = child;
12 } else {
13 right = child;
14 }
15 }

The versions for the BinarySearchTree class are even simpler (Figure 11-22). Since there is only one "child" (the root of the tree), the argument direction is ignored.

With the Parent interface in place, we can write the two-finger method add() (Figure 11-23). If we reach line 17 and have to create a new node, comparison is the direction we last moved.

Figure 11-22. The getChild() and setChild() methods for the BinarySearchTree class.

1 public BinaryNode getChild(int direction) {
2 return root;
3 }
4
5 public void setChild(int direction, BinaryNode child) {
6 root = child;
7 }

Figure 11-23. As with the OrderedList class, the add() method for the BinarySearchTree class is a two-finger algorithm.

 1 public void add(E target) {
 2 Parent parent = this;
 3 BinaryNode node = root;
 4 int comparison = 0;
 5 while (node != null) {
 6 comparison = target.compareTo(node.getItem());
 7 if (comparison < 0) { // Go left
 8 parent = node;
 9 node = node.getLeft();
10 } else if (comparison == 0) { // It's already here
11 return;
12 } else { // Go right
13 parent = node;
14 node = node.getRight();
15 }
16 }
17 parent.setChild(comparison, new BinaryNode(target));
18 }

Deletion

As is usual for Set implementations, the remove() method is the most complicated. The challenge is to make sure the tree is still a binary search tree when we're done with the deletion.

We begin with a search. If it succeeds, we need to get rid of the node containing target.

If the offending node is a leaf, this is easywe just replace the appropriate reference in the parent with null.

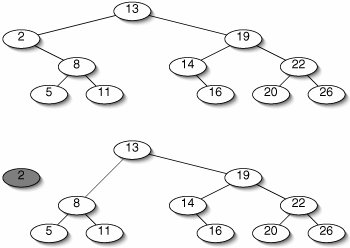
If the node has only one child, we just splice it out much as we would a node in a linked list (Figure 11-24). The one child of the node being removed takes its place. Since all nodes in this subtree are less than the parent of the removed node, the binary search tree is still valid.

Figure 11-24. Before (top) and after (bottom) deleting 2 from a binary search tree. The deleted node's child 8 becomes a child of the deleted node's parent 13.

(This item is displayed on page 302 in the print version)

The complicated case is when the node we want to delete has two children. We can't just splice it out, because then we would be trying to plug in two children where there is room for only one.

Instead, we find some other node which does not have two children, copy the item at that node into this one, and delete the other node (Figure 11-25).

Figure 11-25. Before (top) and after (bottom) deleting 13 from a binary search tree. The node to be deleted has two children, so we can't just splice it out. Instead, we replace its item with the item from another node (14) and delete that node.

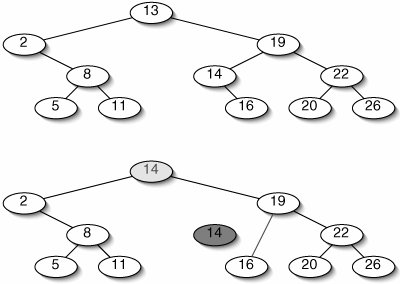
We must be very careful about which node we choose to delete so that the tree will still be a binary search tree. It is always safe to choose the inorder successor of the node we originally wanted to delete. This is the node that would appear next in an inorder traversal of the tree. We can always find a node's inorder successor by going to the right child, then going left until we hit a node with no left child. The inorder successor is not necessarily a leafit can have a right child, it just can't have a left child.

It is safe to replace the node we want to delete with its inorder successor because the inorder successor is the leftmost element in the right subtree. It is therefore larger than anything in the left subtree and smaller than anything else in the right subtree.

The remove() method (Figure 11-26) is another two-finger algorithm. If we find target, we need to modify parent, rather than node. We therefore need to remember the direction we moved when we left parent.

Figure 11-26. The remove() method for the BinarySearchTree class.

 1 public void remove(E target) {
 2 Parent parent = this;
 3 BinaryNode node = root;
 4 int direction = 0;
 5 while (node != null) {
 6 int comparison = target.compareTo(node.getItem());
 7 if (comparison < 0) { // Go left
 8 parent = node;
 9 node = node.getLeft();
10 } else if (comparison == 0) { // Found it
11 spliceOut(node, parent, direction);
12 return;
13 } else { // Go right
14 parent = node;
15 node = node.getRight();
16 }
17 direction = comparison;
18 }
19 }

If target is discovered, remove() invokes spliceOut() (Figure 11-27). The first two cases (lines 912) deal with nodes that do not have two children. For example, if node has no left child (lines 910), node's right child replaces node as a child of parent.

We don't need special code for the case where node is a leaf, because in this situation

parent.setChild(direction, node.getRight());

is equivalent to:

parent.setChild(direction, null);

When node has two children (lines 1315), spliceOut() invokes removeLeftmost() (Figure 11-28). This both removes the leftmost node in the right subtree (the inorder successor) and returns the item from that node, which spliceOut() then installs in the node which was originally to be deleted.

Figure 11-27. The method spliceOut() removes an individual node. If the node has two children, it invokes removeLeftmost().

 1 /**
 2 * Remove node, which is a child of parent. Direction is positive
 3 * if node is the right child of parent, negative if it is the
 4 * left child.
 5 */
 6 protected void spliceOut(BinaryNode node,
 7 Parent parent,
 8 int direction) {
 9 if (node.getLeft() == null) {
10 parent.setChild(direction, node.getRight());
11 } else if (node.getRight() == null) {
12 parent.setChild(direction, node.getLeft());
13 } else {
14 node.setItem(removeLeftmost(node.getRight(), node));
15 }
16 }

Figure 11-28. The method removeLeftmost() both modifies the BinarySearchTree (removing a node) and returns a value (the item in that node).

 1 /**
 2 * Remove the leftmost descendant of node and return the
 3 * item contained in the removed node.
 4 */
 5 protected E removeLeftmost(BinaryNode node, Parent parent) {
 6 int direction = 1;
 7 while (node.getLeft() != null) {
 8 parent = node;
 9 direction = -1;
10 node = node.getLeft();
11 }
12 E result = node.getItem();
13 spliceOut(node, parent, direction);
14 return result;
15 }

BinarySearchTrees should not be used in the plain form explained here. While the average running time for search, insertion, and deletion is logarithmic, the worst-case running time is linear. This worst case occurs if the data are already in order (or in reverse order), causing the tree to be linear. Such data sets are not uncommon. Specifically, the file of legal words for the Anagrams game is probably in alphabetical order, so a BinarySearchTree is no better than an OrderedList.

In Chapters 14 and 17, we will see variations on binary search trees that guarantee logarithmic performance in the worst case.

Exercises

11.6	Expand the definition of a binary search tree to include the possibility of duplicate items.
11.7	Why is it necessary to declare the variable comparison outside the while loop in add() (Figure 11-23), but not in contains() (Figure 11-18) or remove() (Figure 11-26)?
11.8	When an element is added to a binary search tree, a new node is added as a child of an existing node. Before the addition, was this existing node always, sometimes, or never a leaf? Explain.
11.9	In the worst case, searching a binary search tree takes linear time. Can this happen when performing a binary search (Section 8.2) on a sorted array? Explain.
11.10	Suppose a binary search tree is balanced in the sense that the left and right subtrees have the same height. Could deleting the root cause the tree to become imbalanced with the left side taller than the right side? With the right side taller? How would search time for the tree be affected if there were many deletions?
11.11	In remove(), would it be acceptable to replace a node with its inorder predecessor instead of its inorder successor? Explain.