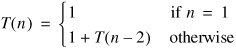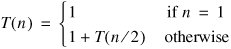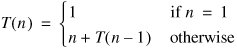Analyzing Recursive Algorithms

Recursive algorithms can be difficult to analyze, because it is not clear how many times they will be invoked. Some new techniques are needed.

Let's start with the LinkedList version of toStringReversedHelper() (Figure 9-12). The corresponding method toStringReversed() will have a running time in the same order, because it only does a constant amount of additional work.

Our standard method of dealing with the if statement doesn't work. If we take the "best-case" branch, we conclude that the algorithm takes constant time. If we take the "worst-case" branch, we conclude that the algorithm never stops! The problem is that our selection of branch depends on n. We always take the first branch for n = 0 and the second for larger values of n. To analyze a recursive algorithm, we must think recursively, in terms of a base case and a recursive case.

The method takes a constant amount of time in the base caselet's call it one step. In the recursive case, it takes one step plus the time for the recursive invocation. We formalize this in an equation called a recurrence. Let T(n) be the time taken to process a chain of n nodes. Then we can write the following recurrence:

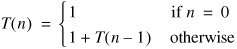
Solving a recurrence means transforming it into an equation with T(n) on the left and no mention of T on the right. In general, solving recurrences can be extremely difficult. However, if we are able to guess the right answer, it is easy to use the recurrence to verify our answer.

In this case, it seems reasonable that toStringReversedHelper() takes time in W(n). Let's guess that T(n) = n. Substituting this into the bottom half of the recurrence, we find:

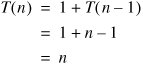
So far, so good. Unfortunately, our guess implies that T(0) = 0, while the recurrence says that T(0) = 1. We got close, but our guess does not work for the base case. It must work exactly to constitute a solution.

Let's try guessing T(n) = n + 1. For the base case:

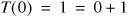
That works. How about the recursive case?

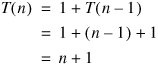
Success! We conclude that toStringReversed() runs in linear time. The ArrayList version has the same recurrence, so it also runs in linear time.

Here is the recurrence for hanoi():

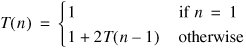
This is more difficult to solve, because there are two recursive calls. We therefore begin by repeatedly expanding the recursive case:

We can draw this expansion out as a recursion tree (Figure 9-15). We start by writing down T(n). We replace this with the time taken in addition to the recursive calls (for this recurrence, 1), and add two copies of T(n 1). We then replace each of these with a 1 and two copies of T(n 2), and so on.

Figure 9-15. Expanding a recursion tree.

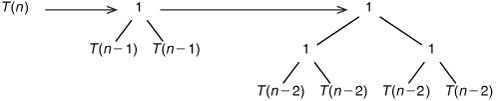
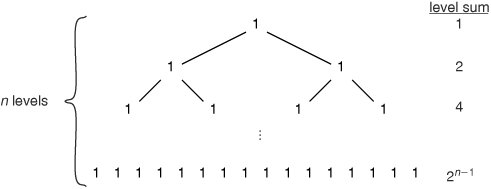
This expansion continues until we have many copies of T(1), which can be replaced with 1. The total running time, then, is the number of 1s in the tree. We can't actually expand the tree all the way without specifying a particular value of n. Instead, we take the sum of the totals on each level of the tree (Figure 9-16). There is 1 step at the top level, 2 at the next level, 4 at the next level, and so on. If we count the top level as level 0, there are 2i steps on level i. There are n levels, corresponding to T(n) down through T(1). The bottommost level is therefore level n 1, consisting of 2n 1 steps.

Figure 9-16. To find the sum of a recursion tree, determine how many steps there are at each level.

The total number of steps in the entire tree is:

Let's verify 2n 1 as a solution to the recurrence.

For the base case, 21 1 = 1, which is correct.

For the recursive case:

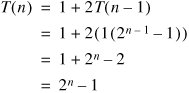
Solved! We conclude that hanoi() takes time in Q(2n).

The recursion tree method can be used to analyze algorithms with only one recursive call. For example, consider the recurrence:

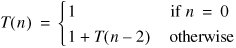
The recursion tree is shown in Figure 9-17. Assuming n is even (Exercise 8.5), we get the solution:

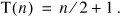
Figure 9-17. When there is only one recursive call, the recursion tree has only one branch.

 

Exercises

9.5	Solve the recurrence below, assuming n is odd.
9.6	Solve the recurrence below, assuming n is a power of 2.
9.7	Solve the recurrence below.
9.8	According to the ancient legend of the Towers of Hanoi, there is a temple where priests are laboring to solve the puzzle with 64 golden disks. When they complete their task, the world will end. Assuming the priests make one move per second, how much time will this take?