The Matrix Class and Transformation

Matrices play a vital role in the transformation process. A matrix is a multidimensional array of values in which each item in the array represents one value of the transformation operation, as we will see in the examples later in this chapter.

In GDI+, the Matrix class represents a 3x2 matrix that contains x, y, and w values in the first, second, and third columns, respectively.

Note

Before using the Matrix class in your applications, you need to add a reference to the System.Drawing.Drawing2D namespace.

We can create a Matrix object by using its overloaded constructors, which take an array of points (hold the matrix items) as arguments. The following code snippet creates three Matrix objects from different overloaded constructors. The first Matrix object has no values for its items. The second and third objects have integer and floating point values, respectively, for the first six items of the matrix.

Matrix M1 = new Matrix();
Matrix M2 = new Matrix(2, 1, 3, 1, 0, 4);
Matrix M3 =
 new Matrix(0.0f, 1.0f, -1.0f, 0.0f, 0.0f, 0.0f);

Table 10.1. Matrix properties

Property	Description
Elements	Returns an array containing matrix elements.
IsIdentity	Returns true if the matrix is an identity matrix; otherwise returns false.
IsInvertible	Returns true if a matrix is invertible; otherwise returns false.
OffsetX	Returns the x translation value of a matrix.
OffsetY	Returns the y translation value of a matrix.

The Matrix class provides properties for accessing and setting its member values. Table 10.1 describes these properties.

The Matrix class provides methods to invert, rotate, scale, and transform matrices. The Invert method is used to reverse a matrix if it is invertible. This method takes no parameters.

Note

The Transform property of the Graphics class is used to apply a transformation in the form of a Matrix object. We will discuss this property in more detail in Section 10.4.

Listing 10.6 uses the Invert method to invert a matrix. We create a Matrix object and read its original values. Then we call the Invert method and read the new values.

Listing 10.6 Inverting a matrix

private void InvertMenu_Click(object sender, System.EventArgs e) { string str = "Original values: "; // Create a Matrix object Matrix X = new Matrix(2, 1, 3, 1, 0, 4); // Write its values for(int i=0; i

The Multiply method multiplies a new matrix against an existing matrix and stores the result in the first matrix. Multiply takes two arguments. The first is the new matrix by which you want to multiply the existing matrix, and the second is an optional MatrixOrder argument that indicates the order of multiplication.

The MatrixOrder enumeration has two values: Append and Prepend. Append specifies that the new operation is applied after the preceding operation; Prepend specifies that the new operation is applied before the preceding operation during cumulative operations. Listing 10.7 multiplies two matrices. We create two Matrix objects and use the Multiply method to multiply the second matrix by the first. Then we read and display the resultant matrix.

Listing 10.7 Multiplying two matrices

private void MultiplyMenu_Click(object sender, System.EventArgs e) { string str = null; // Create two Matrix objects Matrix X = new Matrix(2.0f, 1.0f, 3.0f, 1.0f, 0.0f, 4.0f); Matrix Y = new Matrix(0.0f, 1.0f, -1.0f, 0.0f, 0.0f, 0.0f); // Multiply two matrices X.Multiply(Y, MatrixOrder.Append); // Read the resultant matrix for(int i=0; i

The Reset method resets a matrix to the identity matrix (see Figure 10.21 for an example of an identity matrix). If we call the Reset method and then apply a matrix to transform an object, the result will be the original object.

The Rotate and RotateAt methods are used to rotate a matrix. The Rotate method rotates a matrix at a specified angle. This method takes two arguments: a floating point value specifying the angle, and (optionally) the matrix order. The RotateAt method is useful when you need to change the center of the rotation. Its first parameter is the angle; the second parameter (of type float) specifies the center of rotation. The third (optional) parameter is the matrix order.

Listing 10.8 simply creates a Graphics object using the CreateGraphics method and calls DrawLine and FillRectangle to draw a line and fill a rectangle, respectively.

Listing 10.8 Drawing a line and filling a rectangle

private void Rotate_Click(object sender,
 System.EventArgs e)
{
 // Create a Graphics object
 Graphics g = this.CreateGraphics();
 g.Clear(this.BackColor);
 // Draw a line
 g.DrawLine(new Pen(Color.Green, 3),
 new Point(120, 50),
 new Point(200, 50));
 // Fill a rectangle
 g.FillRectangle(Brushes.Blue,
 200, 100, 100, 60);
 // Dispose of object
 g.Dispose();
}

Figure 10.8 shows the output from Listing 10.8.

Figure 10.8. Drawing a line and filling a rectangle

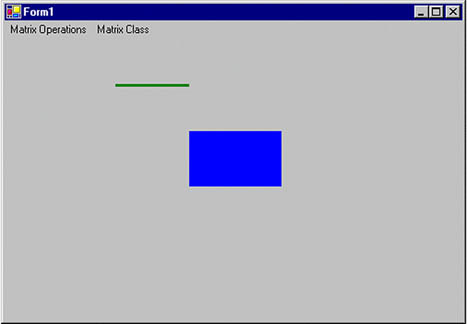
Now let's rotate our graphics objects, using the Matrix object. In Listing 10.9 we create a Matrix object, call its Rotate method to rotate the matrix 45 degrees, and apply the Matrix object to the Graphics object by setting its Transform property.

Listing 10.9 Rotating graphics objects

private void Rotate_Click(object sender,
 System.EventArgs e)
{
 // Create a Graphics object
 Graphics g = this.CreateGraphics();
 g.Clear(this.BackColor);
 // Create a Matrix object
 Matrix X = new Matrix();
 // Rotate by 45 degrees
 X.Rotate(45, MatrixOrder.Append);
 // Apply Matrix object to the Graphics object
 // (i.e., to all the graphics items
 // drawn on the Graphics object)
 g.Transform = X;
 // Draw a line
 g.DrawLine(new Pen(Color.Green, 3),
 new Point(120, 50),
 new Point(200, 50));
 // Fill a rectangle
 g.FillRectangle(Brushes.Blue,
 200, 100, 100, 60);
 // Dispose of object
 g.Dispose();
}

Figure 10.9 shows the new output. Both objects (line and rectangle) have been rotated 45 degrees.

Figure 10.9. Rotating graphics objects

Now let's replace Rotate with RotateAt, as in Listing 10.10.

Listing 10.10 Using the RotateAt method

private void RotateAtMenu_Click(object sender,
 System.EventArgs e)
{
 // Create a Graphics object
 Graphics g = this.CreateGraphics();
 g.Clear(this.BackColor);
 // Create a Matrix object
 Matrix X = new Matrix();
 // Create a point
 PointF pt = new PointF(180.0f, 50.0f);
 // Rotate by 45 degrees
 X.RotateAt(45, pt, MatrixOrder.Append);
 // Apply the Matrix object to the Graphics object
 // (i.e., to all the graphics items
 // drawn on the Graphics object)
 g.Transform = X;
 // Draw a line
 g.DrawLine(new Pen(Color.Green, 3),
 new Point(120, 50),
 new Point(200, 50));
 // Fill a rectangle
 g.FillRectangle(Brushes.Blue,
 200, 100, 100, 60);
 // Dispose of object
 g.Dispose();
}

This new code generates Figure 10.10.

Figure 10.10. Using the RotateAt method

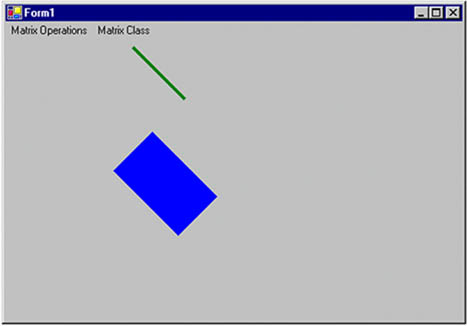
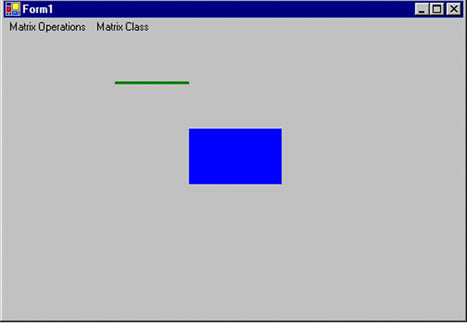
If we call the Reset method in Listing 10.10 after RotateAt and before g.Transform, like this:

X.RotateAt(45, pt, MatrixOrder.Append);
// Reset the matrix
X.Reset();
// Apply the Matrix object to the Graphics object
// (i.e., to all the graphics items
// drawn on the Graphics object)
g.Transform = X;

the revised code generates Figure 10.11, which is the same as Figure 10.8. There is no rotation because the Reset method resets the transformation.

Figure 10.11. Resetting a transformation

The Scale method scales a matrix in the x- and y-directions. This method takes two floating values (scale factors), for the x- and y-axes, respectively. In Listing 10.11 we draw a rectangle with a width of 20 and a height of 30. Then we create a Matrix object and scale it by calling its Scale method with arguments 3 and 4 in the x- and y-directions, respectively.

Listing 10.11 Scaling graphics objects

private void Scale_Click(object sender,
 System.EventArgs e)
{
 // Create Graphics object
 Graphics g = this.CreateGraphics();
 g.Clear(this.BackColor);
 // Draw a filled rectangle with
 // width 20 and height 30
 g.FillRectangle(Brushes.Blue,
 20, 20, 20, 30);
 // Create Matrix object
 Matrix X = new Matrix();
 // Apply 3X scaling
 X.Scale(3, 4, MatrixOrder.Append);
 // Apply transformation on the form
 g.Transform = X;
 // Draw a filled rectangle with
 // width 20 and height 30
 g.FillRectangle(Brushes.Blue,
 20, 20, 20, 30);
 // Dispose of object
 g.Dispose();
}

Figure 10.12 shows the output from Listing 10.11. The first rectangle is the original rectangle; the second rectangle is the scaled rectangle, in which the x position (and width) is scaled by 3, and the y position (and height) is scaled by 4.

Figure 10.12. Scaling a rectangle

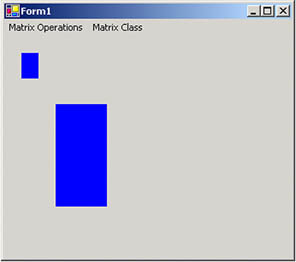
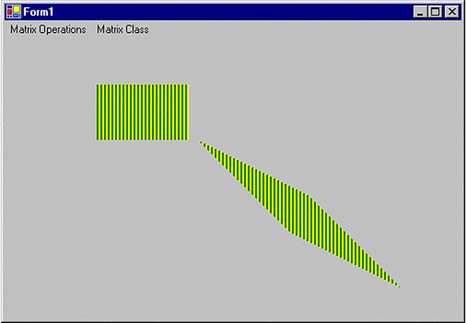
The Shear method provides a shearing transformation and takes two floating point arguments, which represent the horizontal and vertical shear factors, respectively. In Listing 10.12 we draw a filled rectangle with a hatch brush. Then we call the Shear method to shear the matrix by 2 in the vertical direction, and we use Transform to apply the Matrix object.

Listing 10.12 Shearing graphics objects

private void Shear_Click(object sender,
 System.EventArgs e)
{
 // Create a Graphics object
 Graphics g = this.CreateGraphics();
 g.Clear(this.BackColor);
 // Create a brush
 HatchBrush hBrush = new HatchBrush
 (HatchStyle.DarkVertical,
 Color.Green, Color.Yellow);
 // Fill a rectangle
 g.FillRectangle(hBrush,
 100, 50, 100, 60);
 // Create a Matrix object
 Matrix X = new Matrix();
 // Shear
 X.Shear(2, 1);
 // Apply transformation
 g.Transform = X;
 // Fill rectangle
 g.FillRectangle(hBrush,
 10, 100, 100, 60);
 // Dispose of objects
 hBrush.Dispose();
 g.Dispose();
}

Figure 10.13 shows the output from Listing 10.12. The first rectangle in this figure is the original; the second is sheared.

Figure 10.13. Shearing a rectangle

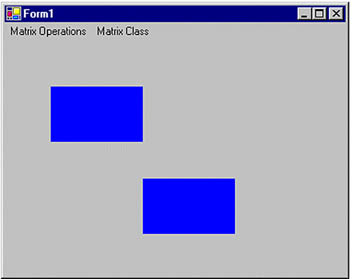
The Translate method translates objects by the specified value. This method takes two floating point arguments, which represent the x and y offsets. For example, Listing 10.13 translates the original rectangle by 100 pixels each in the x- and y-directions.

Listing 10.13 Translating graphics objects

private void Translate_Click(object sender,
 System.EventArgs e)
{
 // Create a Graphics obhect
 Graphics g = this.CreateGraphics();
 g.Clear(this.BackColor);
 // Draw a filled rectangle
 g.FillRectangle(Brushes.Blue,
 50, 50, 100, 60);
 // Create a Matrix object
 Matrix X = new Matrix();
 // Translate by 100 in the x direction
 // and 100 in the y direction
 X.Translate(100, 100);
 // Apply transformation
 g.Transform = X;
 // Draw a filled rectangle after
 // translation
 g.FillRectangle(Brushes.Blue,
 50, 50, 100, 60);
 // Dispose of object
 g.Dispose();
}

Here we draw two rectangles with a width of 100 and a height of 60. Both rectangles start at (50, 50), but the code generates Figure 10.14. Even though the rectangles were drawn with the same size and location, the second rectangle after translation is now located 100 points away in the x- and y-directions from the first rectangle.

Figure 10.14. Translating a rectangle