The Coordinate System

Understanding the coordinate system is another important part of graphics programming. The coordinate system represents the positions of graphic objects on a display device such as a monitor or a printer.

2.2.1 The Cartesian Coordinate System

The Cartesian coordinate system (shown in Figure 2.2) divides a two-dimensional plane into four regions, also called quadrants, and two axes: x and y. The x-axis is represented by a horizontal line and the y-axis by a vertical line. An ordered pair of x and y positions defines a point in a plane. The origin of the plane is a point with x = 0 and y = 0 values, and the quadrants divide the plane relative to the origin.

Figure 2.2. The Cartesian coordinate system

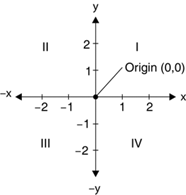
To find out which point falls in which quadrant, we compare the point's x- and y-positions relative to the origin:

Quadrant I: x > 0 and y > 0

Quadrant II: x < 0 and y > 0

Quadrant III: x < 0 and y < 0

Quadrant IV: x > 0 and y < 0

A point with positive x and y values will fall in quadrant I. A point with +y and x values will fall in quadrant II. A point with x and y values will fall in quadrant III, and a point with +x and y values will fall in quadrant IV. For example, a point at coordinates (2, 3) will fall in quadrant IV, and a point at coordinates (3, 2) will fall in quadrant II.

2.2.2 The Default GDI+ Coordinate System

Unlike the Cartesian coordinate system, the default GDI+ coordinate system starts with the origin in the upper left corner. The default x-axis points to the right, and the y-axis points down. As Figure 2.3 shows, the upper left corner starts with points x = 0 and y = 0. Points to the left of x = 0 are negative values in the x-direction, and points above y = 0 are negative values in the y-direction.

Figure 2.3. The GDI+ coordinate system

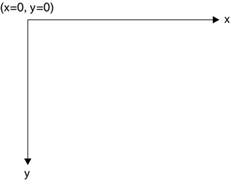
Because the default GDI+ coordinate system starts with (x = 0, y = 0) in the upper left corner of the screen, by default you can see only the points that have positive x and y values. Objects with either x or y values will not be visible on the screen. However, you can apply transformations to move objects with negative values into the visible area.

GDI+ provides three types of coordinate systems: world coordinates, page coordinates, and device coordinates.

1. The coordinate system used in an application is called world coordinates. Suppose that your application draws a line from point A (0, 0) to point B (120, 80), as shown in Figure 2.4. If you don't apply any transformation, the line will be displayed at the right location. Now suppose you want to draw a line from point A (40, 50) to point B (10, 20). The line drawn using these two points will not be displayed on the screen because the GDI+ coordinate system starts at point (0, 0). However, you can transform the coordinates such that (40, 50) is the starting point at the top left corner of the surface.

   Figure 2.4. Drawing a line from point (0, 0) to point (120, 80)

   

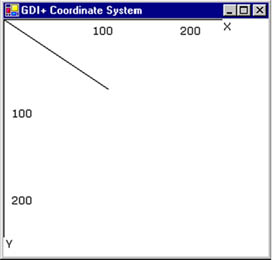
2. The new coordinate system is called page coordinates. The process of converting world coordinates to page coordinates is called the world transformation.
3. You can also control the actual size of graphics objects. For example, if you want to draw a line in inches instead of pixels, you can simply draw a line from point A (1, 1) to point B (1, 2), thereby creating a line that is 1 inch long. The new coordinates are called device coordinates. The process of converting page coordinates to device coordinates is called the page transformation.

We will discuss coordinate systems and transformation in more detail in Chapter 10.