ZERO-PHASE FILTERING
You can cancel the nonlinear phase effects of an IIR filter by following the process shown in Figure 13-31(a). The y(n) output will be a filtered version of x(n) with no filter-induced phase distortion. The same IIR filter is used twice in this scheme, and the time reversal step is a straight left-right flipping of a time-domain sequence. Consider the following. If some spectral component in x(n) has an arbitrary phase of a degrees, and the first filter induces a phase shift of –b degrees, that spectral component's phase at node A will be a–b degrees. The first time reversal step will conjugate that phase and induce an additional phase shift of –q degrees. (Appendix C explains this effect.) Consequently, the component's phase at node B will be –a+b–q degrees. The second filter's phase shift of –b degrees yields a phase of –a–q degrees at node C. The final time reversal step (often omitted in literary descriptions of this zero-phase filtering process) will conjugate that phase and again induce an additional phase shift of –q degrees. Thankfully, the spectral component's phase in y(n) will be a+q–q = a degrees, the same phase as in x(n). This property yields an overall filter whose phase response is zero degrees over the entire frequency range.
Figure 13-31. Two, equivalent, zero-phase filtering techniques.
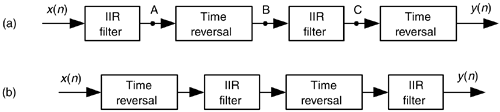
An equivalent zero-phase filter is presented in Figure 13-31(b). Of course, these methods of zero-phase filtering cannot be performed in real time because we can't reverse the flow of time (at least not in our universe). This filtering is a block processing, or off-line process, such as filtering an audio sound file on a computer. We must have all the time samples available before we start processing. The initial time reversal in Figure 13-31(b) illustrates this restriction.
There will be filter transient effects at the beginning and end of the filtered sequences. If transient effects are bothersome in a given application, consider discarding L samples from the beginning and end of the final y(n) time sequence, where L is 4 (or 5) times the order of the IIR filter.
By the way, the final peak-to-peak passband ripple (in dB) of this zero-phase filtering process will be twice the peak-to-peak passband ripple of the single IIR filter. The final stopband attenuation will also be double that of the single filter.
 |
Amazon |  |
