Section G.6. TYPE-IV FSF FREQUENCY RESPONSE
G 6 TYPE IV FSF FREQUENCY RESPONSE
The frequency response of a single-section even-N Type-IV FSF is its transfer function evaluated on the unit circle. To begin that evaluation, we set Eq. (7-23)'s |H(k)| = 1, and denote a Type-IV FSF's single-section transfer function as
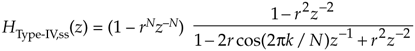
where the "ss" subscript means single-section. Under the assumption that the damping factor r is so close to unity that it can be replaced with 1, we have the simplified FSF transfer function
Equation G-39
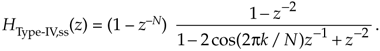
Letting wr = 2pk/N to simplify the notation, and factoring HType-IV,ss(z)'s denominator gives
Equation G-40
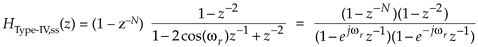
in which we replace each z term with ejw, as
Equation G-41
Factoring out the half-angled exponentials, we have
Equation G-42
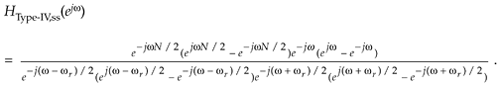
Using Euler's identity, 2jsin(a) = eja – e–ja, we obtain
Equation G-43
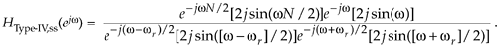
Canceling common factors, and adding like terms, we have
Equation G-44
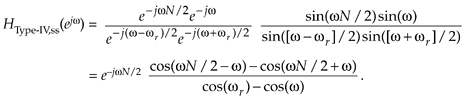
Plugging 2pk/N back in for wr, the single-section frequency response is
Equation G-45
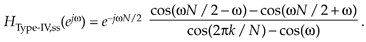
Based on Eq. (G-45), the frequency response of a multisection even-N Type-IV FSF is
Equation G-46
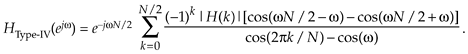
To determine the amplitude response of a single section, we ignore the phase shift terms (complex exponentials) in Eq. (G-45) to yield
Equation G-47
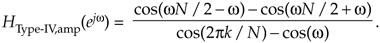
To find the maximum amplitude response at resonance we evaluate Eq. (G-47) when w = 2pk/N, because that's the value of w at the FSF's pole locations. However, that w causes the denominator to go to zero causing the ratio to go to infinity. We move on with one application of L'Hôpital's Rule to Eq. (G-47) to obtain
Equation G-48
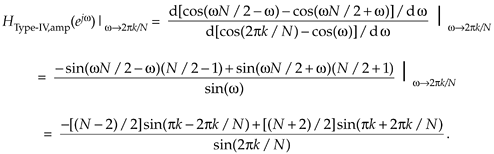
Eliminating the pk terms by using trigonometric reduction formulae sin(pk–a) = (–1)k[-sin(a)] and sin(pk+a) = (–1)k[sin(a)], we have a maximum amplitude response of
Equation G-49
Equation (G-49) is only valid for 1 
k (N/2)–1. Disregarding the (–1)k factors, we have a magnitude response at resonance, as a function of k, of
Equation G-50
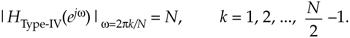
To find the resonant gain at 0 Hz (DC) we set k = 0 in Eq. (G-47), apply L'Hôpital's Rule (the derivative with respect to w) twice, and set w = 0, giving
Equation G-51
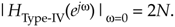
To obtain the resonant gain at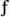 
s/2 Hz we set k = N/2 in Eq. (G-47), again apply L'Hôpital's Rule twice, and set w = p, yielding
Equation G-52
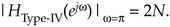
URL http://proquest.safaribooksonline.com/0131089897/app07lev1sec6
 |
Amazon |  |
