Section G.2. SINGLE COMPLEX FSF FREQUENCY RESPONSE
G 2 SINGLE COMPLEX FSF FREQUENCY RESPONSE
The frequency response of a single-section complex FSF is Hss(z) evaluated on the unit circle. We start by substituting ejw for z in Hss(z), because z = ejw defines the unit circle. Given an Hss(z) of

we replace the z terms with ejw, giving
Equation G-7
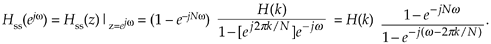
Factoring out the half-angled exponentials e–jwN/2 and e–j(w/2 – pk/N), we have
Equation G-8
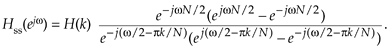
Using Euler's identity, 2jsin(a) = eja – e–ja, we arrive at
Equation G-9
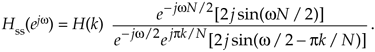
Canceling common factors and rearranging terms in preparation for our final form, we have the desired frequency response of a single-section complex FSF:
Equation G-10
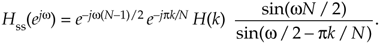
Next we derive the maximum amplitude response of a single-section FSF when its pole is on the unit circle and H(k) = 1. Ignoring those phase shift factors (complex exponentials) in Eq. (G-10), the amplitude response of a single-section FSF is
Equation G-11
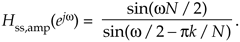
We want to know the value of Eq. (G-11) when w = 2pk/N, because that's the value of w at the pole locations, but |Hss(e jw)|w=2pk/N is indeterminate as
Equation G-12
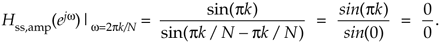
Applying the Marquis de L'Hopital's Rule to Eq. (G-11) yields
Equation G-13

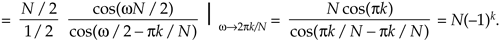
The phase factors in Eq. (G-10), when w = 2pk/N, are
Equation G-14
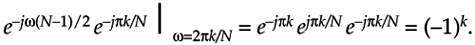
Combining the result of Eqs. (G-13) and (G-14) with Eq. (G-10), we have
Equation G-15
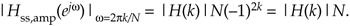
So the maximum magnitude response of a single-section complex FSF at resonance is |H(k)|N, independent of k.
URL http://proquest.safaribooksonline.com/0131089897/app07lev1sec2
 |
Amazon |  |
