FIXED-POINT BINARY FORMATS | Chapter Twelve. Digital Data Formats and Their Effects

Within digital hardware, numbers are represented by binary digits known as bits—in fact, the term bit originated from the words Binary digIT. A single bit can be in only one of two possible states: either a one or a zero.[] A six-bit binary number could, for example, take the form 101101, with the leftmost bit known as the most significant bit (msb), while the rightmost bit is called the least significant bit (lsb). The number of bits in a binary number is known as the word length—hence 101101 has a word length of six. Like the decimal number system so familiar to us, the binary number system assumes a weight associated with each digit in the number. That weight is the base of the system (two for binary numbers and ten for decimal numbers) raised to an integral power. To illustrate this with a simple example, the decimal number 4631 is

[] Binary numbers are used because early electronic computer pioneers quickly realized that it was much more practical and reliable to use electrical devices (relays, vacuum tubes, transistors, etc.) that had only two states, on or off. Thus, the on/off state of a device could represent a single binary digit.

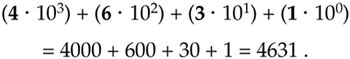
The factors 103, 102, 101, and 100 are the digit weights in Eq. (12-1). Similarly, the six-bit binary number 101101 is equal to decimal 45 as shown by

Equation 12-2

Using subscripts to signify the base of a number, we can write Eq. (12-2) as 1011012 = 4510. Equation (12-2) shows us that, like decimal numbers, binary numbers use the place value system where the position of a digit signifies its weight. If we use B to denote a number system's base, the place value representation of the four-digit number a3a2a1a0 is

Equation 12-3

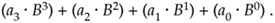
In Eq. (12-3), Bn is the weight multiplier for the digit an, where 0 an B–1. (This place value system of representing numbers is very old—so old, in fact, that its origin is obscure. However, with its inherent positioning of the decimal or binary point, this number system is so convenient and powerful that its importance has been compared to that of the alphabet[1].)

12.1.1 Octal Numbers

As the use of minicomputers and microprocessors rapidly expanded in the 1960s, people grew tired of manipulating long strings of ones and zeros on paper and began to use more convenient ways to represent binary numbers. One way to express a binary number is an octal format, with its base of eight. Converting from binary to octal is as simple as separating the binary number into three-bit groups starting from the right. For example, the binary number 101010012 can be converted to octal format as

Each of the three groups of bits above are easily converted from their binary formats to a single octal digit because, for three-bit words, the octal and decimal formats are the same. That is, starting with the left group of bits, 102 = 210 = 28, 1012 = 510 = 58, and 0012 = 110 = 18. The octal format also uses the place value system meaning that 2518 = (2 · 82 + 5 · 81 + 1 · 80). Octal format enables us to represent the eight-digit 101010012 with the three-digit 2518. Of course, the only valid digits in the octal format are 0 to 7—the digits 8 and 9 have no meaning in octal representation.

12.1.2 Hexadecimal Numbers

Another popular binary format is the hexadecimal number format using 16 as its base. Converting from binary to hexadecimal is done, this time, by separating the binary number into four-bit groups starting from the right. The binary number 101010012 is converted to hexadecimal format as

If you haven't seen the hexadecimal format used before, don't let the A9 digits confuse you. In this format, the characters A, B, C, D, E, and F represent the digits whose decimal values are 10, 11, 12, 13, 14, and 15 respectively. We convert the two groups of bits above to two hexadecimal digits by starting with the left group of bits, 10102 = 1010 = A16, and 10012 = 910 = 916. Hexadecimal format numbers also use the place value system, meaning that A916 = (A · 161 + 9 · 160). For convenience, then, we can represent the eight-digit 101010012 with the two-digit number A916. Table 12-1 lists the permissible digit representations in the number systems discussed thus far.

12.1.3 Fractional Binary Numbers

Fractions (numbers whose magnitudes are greater than zero and less than one) can also be represented by binary numbers if we use a binary point identical in function to our familiar decimal point. In the binary numbers we've discussed so far, the binary point is assumed to be fixed just to the right of the rightmost digit. Using the symbol 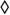to denote the binary point, the six-bit binary fraction 11 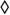0101 is equal to decimal 3.3125 as shown by

Equation 12-4

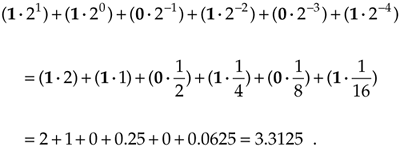
Table 12-1. Allowable Digit Representations vs. Number System Base

Binary	Octal	Decimal	Hexadecimal	Decimal equivalent
0	0	0	0	0
1	1	1	1	1
	2	2	2	2
	3	3	3	3
	4	4	4	4
	5	5	5	5
	6	6	6	6
	7	7	7	7
		8	8	8
		9	9	9
			A	10
			B	11
			C	12
			D	13
			E	14
			F	15

For the example in Eq. (12-4), the binary point is set between the second and third most significant bits. Having a stationary position for the binary point is why binary numbers are often called fixed-point binary.

For some binary number formats (like the floating-point formats that we'll cover shortly), the binary point is fixed just to the left of the most significant bit. This forces the number values to be restricted to the range between zero and one. In this format, the largest and smallest values possible for a b-bit fractional word are 1–2–b and 2–b, respectively. Taking a six-bit binary fraction, for example, the largest value is 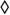1111112, or

Equation 12-5

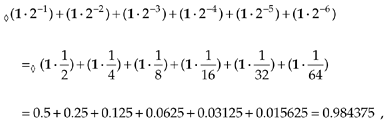
which is in decimal. The smallest nonzero value is 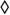0000012, equaling a decimal .

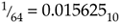12.1.4 Sign-Magnitude Binary Format

For binary numbers to be at all useful in practice, they must be able to represent negative values. Binary numbers do this by dedicating one of the bits in a binary word to indicate the sign of a number. Let's consider a popular binary format known as sign-magnitude. Here, we assume that a binary word's leftmost bit is a sign bit and the remaining bits represent the magnitude of a number which is always positive. For example, we can say that the four-bit number 00112 is +310 and the binary number 10112 is equal to –310, or

Of course, using one of the bits as a sign bit reduces the magnitude of the numbers we can represent. If an unsigned binary number's word length is b bits, the number of different values that can be represented is 2b. An eight-bit word, for example, can represent 28 = 256 different integral values. With zero being one of the values we have to express, a b-bit unsigned binary word can represent integers from 0 to 2b–1. The largest value represented by an unsigned eight-bit word is 28–1 = 25510 = 111111112. In the sign-magnitude binary format a b-bit word can represent only a magnitude of ±2b–1–1, so the largest positive or negative value we can represent by an eight-bit sign-magnitude word is ±28–1–1 = ±127.

12.1.5 Two's Complement Format

Another common binary number scheme, known as the two's complement format, also uses the leftmost bit as a sign bit. The two's complement format is the most convenient numbering scheme from a hardware design standpoint, and has been used for decades. It enables computers to perform both addition and subtraction using the same hardware adder logic. To get the negative version of a positive two's complement number, we merely complement (change a one to a zero and change a zero to a one) each bit and add a one to the complemented word. For example, with 00112 representing a decimal 3 in two's complement format, we obtain a negative decimal 3 through the following steps:

In the two's complement format, a b-bit word can represent positive amplitudes as great as 2b–1–1, and negative amplitudes as large as –2b–1. Table 12-2 shows four-bit word examples of sign-magnitude and two's complement binary formats.

While using two's complement numbers, we have to be careful when adding two numbers of different word lengths. Consider the case where a four-bit number is added to a eight-bit number:

Table 12-2. Binary Number Formats

Decimal equivalent	Sign-magnitude	Two's complement	Offset binary
7	0111	0111	1111
6	0110	0110	1110
5	0101	0101	1101
4	0100	0100	1100
3	0011	0011	1011
2	0010	0010	1010
1	0001	0001	1001
+0	0000	0000	1000
–0	1000	—	—
–1	1001	1111	0111
–2	1010	1110	0110
–3	1011	1101	0101
–4	1100	1100	0100
–5	1101	1011	0011
–6	1110	1010	0010
–7	1111	1001	0001
–8	—	1000	0000

No problem so far. The trouble occurs when our four-bit number is negative. Instead of adding a +3 to the +15, let's try to add a –3 to the +15:

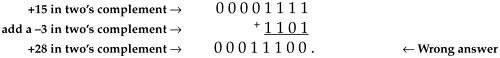
The above arithmetic error can be avoided by performing what's called a sign-extend operation on the four-bit number. This process, typically performed automatically in hardware, extends the sign bit of the four-bit negative number to the left, making it an eight-bit negative number. If we sign-extend the –3 and, then perform the addition, we'll get the correct answer:

12.1.6 Offset Binary Format

Another useful binary number scheme is known as the offset binary format. While this format is not as common as two's complement, it still shows up in some hardware devices. Table 12-2 shows offset binary format examples for four-bit words. Offset binary represents negative numbers by subtracting 2b–1 from an unsigned binary value. For example, in the second row of Table 12-2, the offset binary number is 11102. When this number is treated as an unsigned binary number, it's equivalent to 1410. For four-bit words b = 4 and 2b–1 = 8, so 1410 – 810 = 610, which is the decimal equivalent of 11102 in offset binary. The difference between the unsigned binary equivalent and the actual decimal equivalent of the offset binary numbers in Table 12-2 is always –8. This kind of offset is sometimes referred to as a bias when the offset binary format is used. (It may interest the reader that we can convert back and forth between the two's complement and offset binary formats merely by complementing a word's most significant bit.)

The history, arithmetic, and utility of the many available number formats is a very broad field of study. A thorough and very readable discussion of the subject is given by Knuth in Reference [2].

URL http://proquest.safaribooksonline.com/0131089897/ch12lev1sec1