Chapter Six. Infinite Impulse Response Filters
Six Infinite Impulse Response Filters
Infinite impulse response (IIR) digital filters are fundamentally different from FIR filters because practical IIR filters always require feedback. Where FIR filter output samples depend only on past input samples, each IIR filter output sample depends on previous input samples and previous filter output samples. IIR filters' memory of past outputs is both a blessing and a curse. Like all feedback systems, perturbations at the IIR filter input could, depending on the design, cause the filter output to become unstable and oscillate indefinitely. This characteristic of possibly having an infinite duration of nonzero output samples, even if the input becomes all zeros, is the origin of the phrase infinite impulse response. It's interesting at this point to know that, relative to FIR filters, IIR filters have more complicated structures (block diagrams), are harder to design and analyze, and do not have linear phase responses. Why in the world, then, would anyone use an IIR filter? Because they are very efficient. IIR filters require far fewer multiplications per filter output sample to achieve a given frequency magnitude response. From a hardware standpoint, this means that IIR filters can be very fast, allowing us to build real-time IIR filters that operate over much higher sample rates than FIR filters.[ ]
]
[
] At the end of this chapter, we briefly compare the advantages and disadvantages of IIR filters relative to FIR filters.
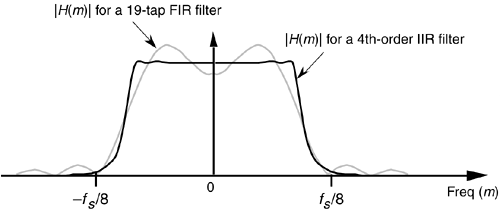
To illustrate the utility of IIR filters, Figure 6-1 contrasts the frequency magnitude responses of what's called a fourth-order low-pass IIR filter and the 19-tap FIR filter of Figure 5-19(b) from Chapter 5. Where the 19-tap FIR filter in Figure 6-1 requires 19 multiplications per filter output sample, the fourth-order IIR filter requires only 9 multiplications for each filter output sample. Not only does the IIR filter give us reduced passband ripple and a sharper filter roll-off, it does so with less than half the multiplication workload of the FIR filter.
Figure 6-1. Comparison of the frequency magnitude responses of a 19-tap low-pass FIR filter and a 4th-order low-pass IIR filter.
Recall from Section 5.3 that, to force an FIR filter's frequency response to have very steep transition regions, we had to design an FIR filter with a very long impulse response. The longer the impulse response, the more ideal our filter frequency response will become. From a hardware standpoint, the maximum number of FIR filter taps we can have (the length of the impulse response) depends on how fast our hardware can perform the required number of multiplications and additions to get a filter output value before the next filter input sample arrives. IIR filters, however, can be designed to have impulse responses that are longer than their number of taps! Thus, IIR filters can give us much better filtering for a given number of multiplications per output sample than FIR filters. With this in mind, let's take a deep breath, flex our mathematical muscles, and learn about IIR filters.
 |
Amazon |  |
