SIMPLIFIED FIR FILTER STRUCTURE
If we implement a linear phase FIR digital filter using the standard structure in Figure 13-16(a), there's a way to reduce the number of multipliers when the filter has an odd number of taps. Let's look at the top of Figure 13-16(a) where the five-tap FIR filter coefficients are h(0) through h(4) and the y(n) output is
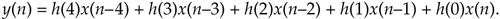
Figure 13-16. Conventional and simplified structures of an FIR filter: (a) with an odd number of taps; (b) with an even number of taps.
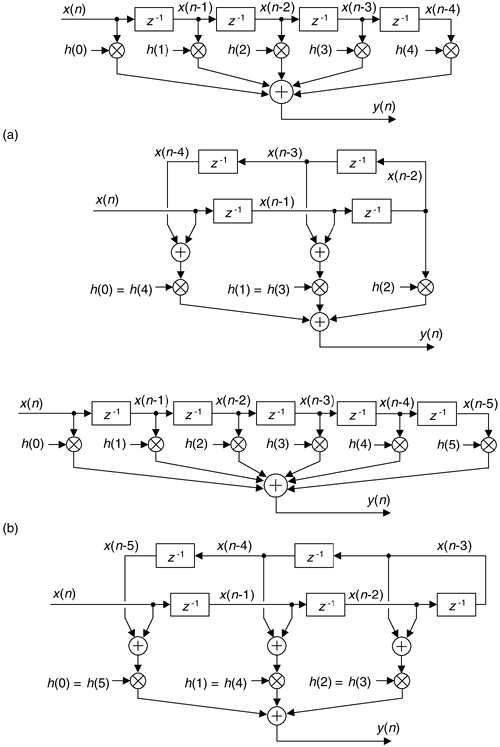
If the FIR filter's coefficients are symmetrical we can reduce the number of necessary multipliers. That is, if h(4) = h(0), and h(3) = h(1), we can implement Eq. (13-62) by
Equation 13-63
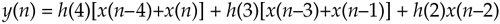
where only three multiplications are necessary as shown at the bottom of Figure 13-16(a). In our five-tap filter case, we've eliminated two multipliers at the expense of implementing two additional adders. This minimum-multiplier structure is called a "folded" FIR filter.
In the general case of symmetrical-coefficient FIR filters with S taps, we can trade (S–1)/2 multipliers for (S–1)/2 adders when S is an odd number. So in the case of an odd number of taps, we need only perform (S–1)/2 + 1 multiplications for each filter output sample. For an even number of symmetrical taps as shown in Figure 13-16(b), the savings afforded by this technique reduces the necessary number of multiplications to S/2.
As of this writing, typical programmable-DSP chips cannot take advantage of the folded FIR filter structure because it requires a single addition before each multiply and accumulate operation.
URL http://proquest.safaribooksonline.com/0131089897/ch13lev1sec7
 |
Amazon |  |
