RELATIONSHIP OF THE FFT TO THE DFT
Although many different FFT algorithms have been developed, in this section we'll see why the radix-2 FFT algorithm is so popular and learn how it's related to the classical DFT algorithm. The radix-2 FFT algorithm is a very efficient process for performing DFTs under the constraint that the DFT size be an integral power of two. (That is, the number of points in the transform is N = 2k, where k is some positive integer.) Let's see just why the radix-2 FFT is the favorite spectral analysis technique used by signal-processing practitioners.
Recall that our DFT Example 1 in Section 3.1 illustrated the number of redundant arithmetic operations necessary for a simple 8-point DFT. (For example, we ended up calculating the product of 1.0607 · 0.707 four separate times.) On the other hand, the radix-2 FFT eliminates these redundancies and greatly reduces the number of necessary arithmetic operations. To appreciate the FFT's efficiency, let's consider the number of complex multiplications necessary for our old friend, the expression for an N-point DFT,
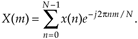
For an 8-point DFT, Eq. (4-1) tells us that we'd have to perform N2 or 64 complex multiplications. (That's because, for each of the eight X(m)s, we have to sum eight complex products as n goes from 0 to 7.) As we'll verify in later sections of this chapter, the number of complex multiplications, for an N-point FFT, is approximately
Equation 4-2

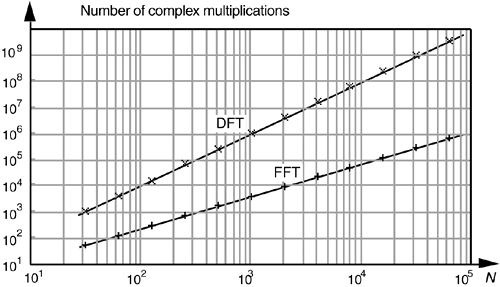
(We say approximately because some multiplications turn out to be multiplications by +1 or –1, which amount to mere sign changes.) Well, this (N/2)log2N value is a significant reduction from the N2 complex multiplications required by Eq. (4-1), particularly for large N. To show just how significant, Figure 4-1 compares the number of complex multiplications required by DFTs and radix-2 FFTs as a function of the number of input data points N. When N = 512, for example, the DFT requires 200 times more complex multiplications than those needed by the FFT. When N = 8192, the DFT must calculate 1000 complex multiplications for each complex multiplication in the FFT!
Figure 4-1. Number of complex multiplications in the DFT and the radix-2 FFT as a function of N.
Here's my favorite example of the efficiency of the radix-2 FFT. Say you perform a two million-point FFT (N = 2,097,152) on your desktop computer and it takes 10 seconds. A two million-point DFT on the other hand, using your computer, will take more than three weeks! The publication and dissemination of the radix-2 FFT algorithm was, arguably, the most important event in digital signal processing.
It's appropriate now to make clear that the FFT is not an approximation of the DFT. It's exactly equal to the DFT; it is the DFT. Moreover, all of the performance characteristics of the DFT described in the previous chapter, output symmetry, linearity, output magnitudes, leakage, scalloping loss, etc., also describe the behavior of the FFT.
URL http://proquest.safaribooksonline.com/0131089897/ch04lev1sec1
 |
Amazon |  |
