COMPUTING THE INVERSE FFT USING THE FORWARD FFT
There are many signal processing applications where the capability to perform the inverse FFT is necessary. This can be a problem if available hardware, or software routines, have only the capability to perform the forward FFT. Fortunately, there are two slick ways to perform the inverse FFT using the forward FFT algorithm.
13.6.1 Inverse FFT Method 1
The first inverse FFT calculation scheme is implemented following the processes shown in Figure 13-14.
Figure 13-14. Processing for first inverse FFT calculation method.
To see how this works, consider the expressions for the forward and inverse DFTs. They are
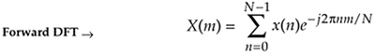
Equation 13-52
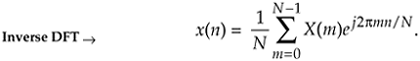
To reiterate our goal, we want to use the process in Eq. (13-51) to implement Eq. (13-52). The first step of our approach is to use complex conjugation. Remember, conjugation (represented by the superscript * symbol) is the reversal of the sign of a complex number's imaginary exponent—if x = ejø, then x* = e–jø. So, as a first step we take the complex conjugate of both sides of Eq. (13-52) to give us
Equation 13-53
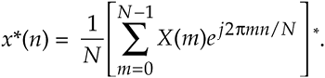
One of the properties of complex numbers, discussed in Appendix A, is that the conjugate of a product is equal to the product of the conjugates. That is, if c = ab, then c* = (ab)* = a*b*. Using this, we can show the conjugate of the right side of Eq. (13-53) to be
Equation 13-54
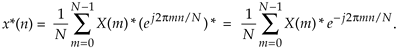
Hold on; we're almost there. Notice the similarity of Eq. (13-54) to our original forward DFT expression Eq. (13-51). If we perform a forward DFT on the conjugate of the X(m) in Eq. (13-54), and divide the results by N, we get the conjugate of our desired time samples x(n). Taking the conjugate of both sides of Eq. (13-54), we get a more straightforward expression for x(n):
Equation 13-55
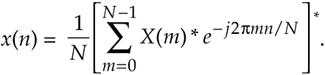
13.6.2 Inverse FFT Method 2
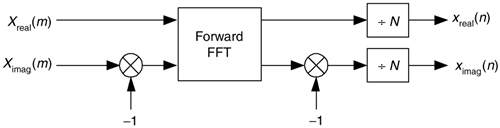
The second inverse FFT calculation technique is implemented following the interesting data flow shown in Figure 13-15.
Figure 13-15. Processing for second inverse FFT calculation method.

In this clever inverse FFT scheme we don't bother with conjugation. Instead, we merely swap the real and imaginary parts of sequences of complex data[21]. To see why this process works, let's look at the inverse DFT equation again while separating the input X(m) term into its real and imaginary parts and remembering that ejø = cos(ø) + jsin(ø).
Equation 13-56

Multiplying the complex terms in Eq. (13-56) gives us
Equation 13-57
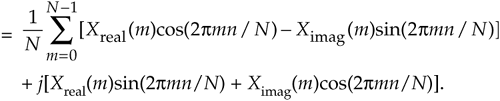
Equation (13-57) is the general expression for the inverse DFT and we'll now quickly show that the process in Figure 13-15 implements this equation. With X(m) = Xreal(m) + jXimag(m), then swapping these terms gives us
Equation 13-58
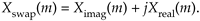
The forward DFT of our Xswap(m) is
Equation 13-59
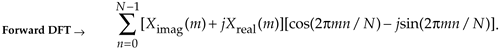
Multiplying the complex terms in Eq. (13-59) gives us
Equation 13-60

Swapping the real and imaginary parts of the results of this forward DFT gives us what we're after:
Equation 13-61
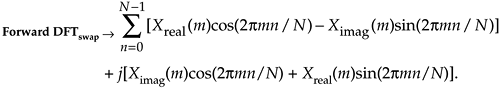
If we divided Eq. (13-61) by N, it would be exactly equal to the inverse DFT expression in Eq. (13-57), and that's what we set out to show.
URL http://proquest.safaribooksonline.com/0131089897/ch13lev1sec6
 |
Amazon |  |
