Chapter Eight. Quadrature Signals
Eight Quadrature Signals
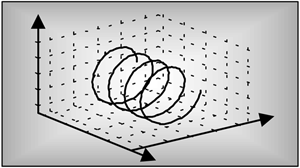
Quadrature signals are based on the notion of complex numbers. Perhaps no other topic causes more heartache for newcomers to DSP than these numbers and their strange terminology of j-operator, complex, analytic, imaginary, real, and orthogonal. If you're a little unsure of the physical meaning of complex numbers and the j =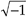 
operator, don't feel bad because you're in good company. Sixteenth century Italian mathematician Girolamo Cardano described an imaginary number "as subtle as it is useless." In the 17th century Gottfried Leibniz described imaginary numbers as being "amphibian, halfway between existence and nonexistence." (The term "imaginary" was first used by the brilliant mathematician/philosopher René Descartes in the 17th century, and was meant to be derogatory. That's because not only was the notion of the square root of a negative number dubious at best, surprisingly there was no consensus at that time as to the true meaning of negative real numbers.) Even Karl Gauss, one the world's greatest mathematicians, called the j-operator the "shadow of shadows." Here we'll shine some light on that shadow so you'll never have to call the Quadrature Psychic Hotline for help.
Quadrature signals, represented by complex numbers, are used in just about every field of science and engineering.[
] Quadrature signals are of interest to us because they describe the effects of Fourier analysis as well as the quadrature processing and implementations that take place in modern digital communications systems. In this chapter we'll review the fundamentals of complex numbers and get comfortable with how they're used to represent quadrature signals. Next we'll examine the notion of negative frequency as it relates to quadrature signal algebraic notation, and learn to speak the language of quadrature processing. In addition, we'll use three-dimensional time and frequency-domain plots to clarify and give physical meaning to quadrature signals.
[
 |
Amazon |  |
