Section G.5. REAL FSF TRANSFER FUNCTION
G 5 REAL FSF TRANSFER FUNCTION
The transfer function equation for the real-valued multisection FSF looks a bit strange at first glance, so rather than leaving its derivation as an exercise for the reader, we show the algebraic acrobatics necessary in its development. To preview our approach, we'll start with the transfer function of a multisection complex FSF and define the H(k) gain factors such that all filter poles are in conjugate pairs. This will lead us to real-FSF structures with real-valued coefficients. With that said, we begin with Eq. (7-18)'s transfer function of a guaranteed-stable N-section complex FSF of
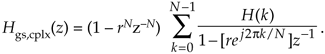
Assuming N is even, and breaking Eq. (G-29)'s summation into parts, we can write
Equation G-30
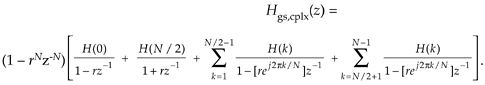
The first two ratios inside the brackets account for the k = 0 and k = N/2 frequency samples. The first summation is associated with the positive frequency range, which is the upper half of the z-plane's unit circle. The second summation is associated with the negative frequency range, the lower half of the unit circle.
To reduce the clutter of our derivation, let's identify the two summations as
Equation G-31
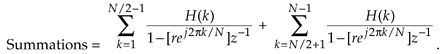
We then combine the summations by changing the indexing of the second summation as
Equation G-32
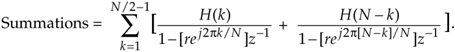
Putting those ratios over a common denominator and multiplying the denominator factors, and then forcing the H(N–k) gain factors to be complex conjugates of the H(k) gain factors, we write
Equation G-33

where the "*" symbol means conjugation. Defining H(N-k) = H*(k) mandates that all poles will be conjugate pairs and, as we'll see, this condition converts our complex FSF into a real FSF with real-valued coefficients. Plowing forward, because ej2p[N–k]/N = e–j2pN/Ne–j2pk/N = e–j2pk/N, we make that substitution in Eq. (G-33), rearrange the numerator, and combine the factors of z-1 in the denominator to arrive at
Equation G-34

Next we define each complex H(k) in rectangular form with an angle fk, or H(k) = |H(k)|[cos(fk) +jsin(fk)], and H*(k) = |H(k)|[cos(fk) –jsin(fk)]. Realizing that the imaginary parts of the sum cancel so that H(k) + H*(k) = 2|H(k)|cos(fk) allows us to write
Equation G-35

Recalling Euler's identity, 2cos(a) = eja + e–ja, and combining the |H(k)| factors leads to the final form of our summation:
Equation G-36
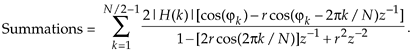
Substituting Eq. (G-36) for the two summations in Eq. (G-30), we conclude with the desired transfer function
Equation G-37
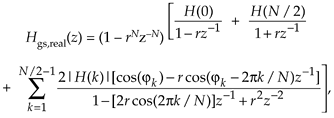
where the subscript "real" means a real-valued multisection FSF.
URL http://proquest.safaribooksonline.com/0131089897/app07lev1sec5
 |
Amazon |  |
