INVERSE DFT
Although the DFT is the major topic of this chapter, it's appropriate, now, to introduce the inverse discrete Fourier transform (IDFT). Typically we think of the DFT as transforming time-domain data into a frequency-domain representation. Well, we can reverse this process and obtain the original time- domain signal by performing the IDFT on the X(m) frequency-domain values. The standard expressions for the IDFT are
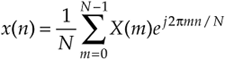
and equally,
Equation 3-23'
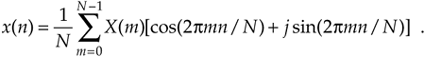
Remember the statement we made in Section 3.1 that a discrete time- domain signal can be considered the sum of various sinusoidal analytical frequencies and that the X(m) outputs of the DFT are a set of N complex values indicating the magnitude and phase of each analysis frequency comprising that sum. Equations (3-23) and (3-23') are the mathematical expressions of that statement. It's very important for the reader to understand this concept. If we perform the IDFT by plugging our results from DFT Example 1 into Eq. (3-23), we'll go from the frequency-domain back to the time-domain and get our original real Eq. (3-11') x(n) sample values of
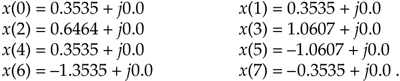
Notice that Eq. (3-23)'s IDFT expression differs from the DFT's Eq. (3-2) only by a 1/N scale factor and a change in the sign of the exponent. Other than the magnitude of the results, every characteristic that we've covered thus far regarding the DFT also applies to the IDFT.
URL http://proquest.safaribooksonline.com/0131089897/ch03lev1sec7
 |
Amazon |  |
