Section G.3. MULTISECTION COMPLEX FSF PHASE
G 3 MULTISECTION COMPLEX FSF PHASE
This appendix shows how the (-1)k factors arise in Eq. (7-13) for an even-N multisection linear-phase complex FSF. Substituting the positive-frequency, 0 
k (N/2)–1, |H(k)|ejf(k) gain factors, with f(k) phase values from Eq. (7-11), into Eq. (7-10) gives
where the subscript "pf" means positive frequency. Focusing only on the numerator inside the summation in Eq. (G-16), it is
Equation G-17
showing how the (–1)k factors occur within the first summation of Eq. (7-13). Next we substitute the negative-frequency |H(k)|ejf(k) gain factors, (N/2)+1 k N–1, with f(k) phase values from Eq. (7-11''), into Eq. (7-10) giving
Equation G-18
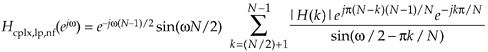
where the subscript "nf" means negative frequency. Again, looking only at the numerator inside the summation in Eq. (G-18), it is
Equation G-19
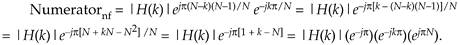
That ejpN factor in Eq. (G-19) is equal to 1 when N is even, so we write
Equation G-20
establishing both the negative sign before, and the (–1)k factor within, the second summation of Eq. (7-13). To account for the single-section for the k = N/2 term (this is the Nyquist, or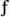 
s/2, frequency, where w = p) we plug the |H(N/2)|ej0 gain factor, and k = N/2, into Eq. (7-8) giving
Equation G-21
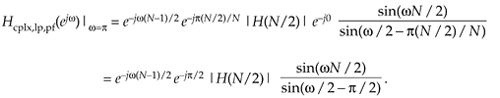
URL http://proquest.safaribooksonline.com/0131089897/app07lev1sec3
 |
Amazon |  |
