THE NOTATION OF COMPLEX NUMBERS | Chapter Eight. Quadrature Signals

To establish our terminology, we define real numbers to be those numbers we use in everyday life, like a voltage, a temperature on the Fahrenheit scale, or the balance of your checking account. These one-dimensional numbers can be either positive or negative, as depicted in Figure 8-1(a). In that figure we show a one-dimensional axis and say a single real number can be represented by a point on the axis. Out of tradition, let's call this axis the real axis.

Figure 8-1. Graphical interpretations: (a) a real number; (b) a complex number.

A complex number c is shown in Figure 8-1(b) where it's also represented as a point. Complex numbers are not restricted to lying on a one-dimensional line, but can reside anywhere on a two-dimensional plane. That plane is called the complex plane (some mathematicians like to call it an Argand diagram), and it enables us to represent complex numbers having both real and imaginary parts. For example in Figure 8-1(b), the complex number c = 2.5 + j2 is a point lying on the complex plane on neither the real nor the imaginary axis. We locate point c by going +2.5 units along the real axis and up +2 units along the imaginary axis. Think of those real and imaginary axes exactly as you think of the East-West and North-South directions on a road map.

We'll use a geometric viewpoint to help us understand some of the arithmetic of complex numbers. Taking a look at Figure 8-2, we can use the trigonometry of right triangles to define several different ways of representing the complex number c.

Figure 8-2. The phasor representation of complex number c = a + jb on the complex plane.

Our complex number c is represented in a number of different ways in the literature, such as shown in Table 8-1.

Eqs. (8-3) and (8-4) remind us that c can also be considered the tip of a phasor on the complex plane, with magnitude M, in the direction of ø degrees relative to the positive real axis as shown in Figure 8-2. Keep in mind that c is a complex number and the variables a, b, M, and ø are all real numbers. The magnitude of c, sometimes called the modulus of c, is

Table 8-1. Complex Number Notation

Notation name	Math expression	Remarks
Rectangular form	c = a + jb	Used for explanatory purposes. Easiest to understand. (Also called the Cartisian form.)	(8–1)
Trigonometric form	c = M[cos(ø) + jsin(ø)]	Commonly used to describe quadrature signals in communications systems.	(8–2)
Polar form	c = Mejø	Most puzzling, but the primary form used in math equations. (Also called the Exponential form. Sometimes written as Mexp(jø).)	(8–3)
Magnitude-angle form	c = Mø	Used for descriptive purposes, but too cumbersome for use in algebraic equations. (Essentially a shorthand version of Eq. (8-3).)	(8–4)

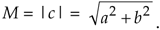
The phase angle ø, the argument of c, is the arctangent of the ratio of the imaginary part over the real part, or

Equation 8-6

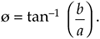
If we set Eq. (8-3) equal to Eq. (8-2), Mejø = M[cos(ø) + jsin(ø)] , we can state what's named in his honor and now called one of Euler's identities as:

Equation 8-7

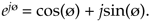
The suspicious reader should now be asking, "Why is it valid to represent a complex number using that strange expression of the base of the natural logarithms, e, raised to an imaginary power?" We can validate Eq. (8-7) as did Europe's wizard of infinite series, Leonhard Euler, by plugging jø in for z in the series expansion definition of ez in the top line of Figure 8-3.[] That substitution is shown on the second line. Next we evaluate the higher orders of j to arrive at the series in the third line in the figure. Those of you with elevated math skills like Euler (or who check some math reference book) will recognize that the alternating terms in the third line are the series expansion definitions of the cosine and sine functions.

[] Leonhard Euler, born in Switzerland in 1707, is considered by many historians to be the world's greatest mathematician. By the way, the name Euler is pronounced as "oiler."

Figure 8-3. One derivation of Euler's equation using series expansions for ez, cos(ø), and sin(ø).

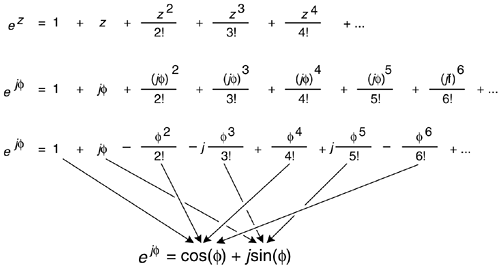
Figure 8-3 verifies Eq. (8-7) and justifies our representation of a complex number using the Eq. (8-3) polar form: Mejø. If we substitute –jø for z in the top line of Figure 8-3, we end up with a slightly different, and very useful, form of Euler's identity:

Equation 8-8

The polar form of Eqs. (8-7) and (8-8) benefits us because:

It simplifies mathematical derivations and analysis, turning trigonometric equations into the simple algebra of exponents. Math operations on complex numbers follow exactly the same rules as real numbers.
It makes adding signals merely the addition of complex numbers (vector addition).
It's the most concise notation.
It's indicative of how digital communications system are implemented, and described in the literature.

Here's a quick example of how the polar form of complex numbers can simplify a mathematical analysis. Let's say we wanted to understand the process of multiplying complex number c1 = cos(ø) + jsin(ø) by another complex number, c2 = cos(2ø) – jsin(2ø), whose angle is the negative of twice c1's angle. The product is

Equation 8-9

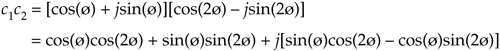
Using the trigonometric function product identities, we can write Eq. (8-9) as

Equation 8-10

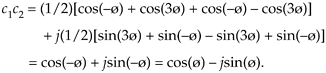
So the c1c2 product yields the complex conjugate of c1. That's not too thrilling, but what is interesting is how trivial a polar form c1c2 product analysis turns out to be. We can complete our polar form analysis in one brief line:

Equation 8-11

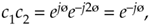
which is equivalent to Eq. (8-10). For math analysis, polar form is usually the notation of choice.

Back to quadrature signals. We'll be using Eqs. (8-7) and (8-8) to understand the nature of time-domain quadrature signals. But first let's take a deep breath and enter the Twilight Zone of the j operator.

You've seen the definition j = 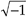before. Stated in words, we say that j represents a number that when multiplied by itself results in a negative one. Well, this definition causes difficulty for the beginner because we all know that any number multiplied by itself always results in a positive number. (Unfortunately, engineering textbooks often define j and then, with justified haste, swiftly carry on with all the ways the j operator can be used to analyze sinusoidal signals. Readers soon forget about the question: What does j = 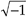actually mean?) Well, 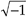had been on the mathematical scene for some time, but wasn't taken seriously until it had to be used to solve cubic polynomial equations in the sixteenth century[1,2]. Mathematicians reluctantly began to accept the abstract concept of 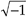without having to visualize it, because its mathematical properties were consistent with the arithmetic of normal real numbers.

It was Euler's equating complex numbers to real sines and cosines, and Gauss' brilliant introduction of the complex plane, that finally legitimized the notion of 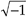to Europe's mathematicians in the eighteenth century. Euler, going beyond the province of real numbers, showed that complex numbers had a clean consistent relationship to the well known real trigonometric functions of sines and cosines. As Einstein showed the equivalence of mass and energy, Euler showed the equivalence of real sines and cosines to complex numbers. Just as modern-day physicists don't know what an electron is but they understand its properties, we'll not worry about what j is and be satisfied with understanding its behavior. We'll treat j not as a number, but as an operation performed on a number, as we do with negation or multiplication. For our purposes, the j-operator means rotate a complex number by 90o counterclockwise. (For our friends in the UK, counterclockwise means your anti-clockwise.) Let's see why.

We'll get comfortable with the complex plane representation of imaginary numbers by examining the mathematical properties of the j = 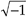operator as shown in Figure 8-4.

Figure 8-4. What happens to the real number 8 when multiplied by j and -j.

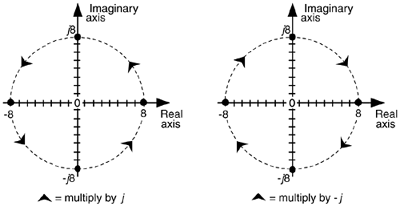
Multiplying any number on the real axis by j results in an imaginary product lying on the imaginary axis. The example on the left in Figure 8-4 shows that if +8 is represented by the dot lying on the positive real axis, multiplying +8 by j results in an imaginary number, +j8, whose position has been rotated 90o counterclockwise (from +8), putting it on the positive imaginary axis. Similarly, multiplying +j8 by j results in another 90o rotation, yielding the -8 lying on the negative real axis because j2 = –1. Multiplying –8 by j results in a further 90o rotation giving the –j8 lying on the negative imaginary axis. Whenever any number represented by a dot is multiplied by j the result is a counterclockwise rotation of 90o. (Conversely, multiplication by –j results in a clockwise rotation of –90o on the complex plane.)

If we let ø = p/2 in Eq. 8-7, we can say

Equation 8-12

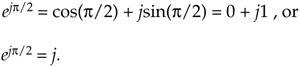
Here's the point to remember. If you have a single complex number, represented by a point on the complex plane, multiplying that number by j or by ejp/2 will result in a new complex number rotated 90o counterclockwise (CCW) on the complex plane. Don't forget this, as it will be useful as you begin reading the literature of quadrature processing systems!

Let's pause for a moment here to catch our breath. Don't worry if the ideas of imaginary numbers and the complex plane seem a little mysterious. It's that way for everyone at first—you'll get comfortable with them the more you use them. (Remember, the j-operator puzzled Europe's heavyweight mathematicians for many years.) Granted, not only is the mathematics of complex numbers a bit strange at first, but the terminology is almost bizarre. While the term imaginary is an unfortunate one to use, the term complex is downright weird. When first encountered, the phrase complex numbers makes us think complicated numbers. This is regrettable because the concept of complex numbers is not really so complicated.[] Just know that the purpose of the above mathematical rigamarole was to validate Eqs. (8-2), (8-3), (8-7), and (8-8). Now, let's (finally!) talk about time-domain signals.

[] The brilliant American engineer Charles P. Steinmetz, who pioneered the use of real and imaginary numbers in electrical circuit analysis in the early twentieth century, refrained from using the term complex numbers—he called them general numbers.

URL http://proquest.safaribooksonline.com/0131089897/ch08lev1sec2