BANDPASS QUADRATURE SIGNALS IN THE FREQUENCY DOMAIN
In quadrature processing, by convention, the real part of the spectrum is called the in-phase component and the imaginary part of the spectrum is called the quadrature component. The signals whose complex spectra are in Figure 8-12(a), (b), and (c) are real, and in the time domain they can be represented by amplitude values having nonzero real parts and zero-valued imaginary parts. We're not forced to use complex notation to represent them in the time domain—the signals are real only.
Figure 8-12. Quadrature representation of signals: (a) real sinusoid cos(2pfot + ø); (b) real bandpass signal containing six sinusoids over bandwidth B; (c) real bandpass signal containing an infinite number of sinusoids over bandwidth B Hz; (d) complex bandpass signal of bandwidth B Hz.
Real signals always have positive and negative frequency spectral components. For any real signal, the positive and negative frequency components of its in-phase (real) spectrum always have even symmetry around the zero-frequency point. That is, the in-phase part's positive and negative frequency components are mirror images of each other. Conversely, the positive and negative frequency components of its quadrature (imaginary) spectrum are always negatives of each other. This means that the phase angle of any given positive quadrature frequency component is the negative of the phase angle of the corresponding quadrature negative frequency component as shown by the thin solid arrows in Figure 8-12(a). This conjugate symmetry is the invariant nature of real signals, and is obvious when their spectra are represented using complex notation.
A complex-valued time signal, whose spectrum can be that in Figure 8-12(d), is not restricted to the above spectral conjugate symmetry conditions. We'll call that special complex signal an analytic signal, signifying that it has no negative-frequency spectral components.
Let's remind ourselves again: those bold arrows in Figure 8-12(a) and (b) are not rotating phasors. They're frequency-domain impulses indicating a single complex exponential ej2pft. The directions in which the impulses are pointing show the relative phases of the spectral components.
There's an important principle to keep in mind before we continue. Multiplying a time signal by the complex exponential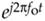 
, what we call quadrature mixing (also called complex mixing) shifts a signal's spectrum upward in frequency by fo Hz, as shown in Figure 8-13(a) and (b). Likewise, multiplying a time signal by 
(also called complex down-conversion or mixing to baseband) shifts a signal's spectrum down to a center frequency of zero Hz as shown in Figure 8-13(c). The process of quadrature mixing is used in many DSP applications as well as most modern-day digital communications systems.
Figure 8-13. Quadrature mixing of a bandpass signal: (a) spectrum of a complex signal x(t); (b) spectrum of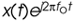 
; (c) spectrum of 
.
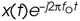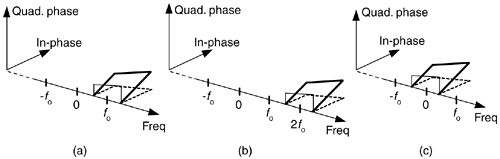
Our entire quadrature signals discussion, thus far, has been based on continuous signals, but the principles described here apply equally well to discrete-time signals. Let's look at the effect of complex down-conversion of a discrete signal's spectrum.
 |
Amazon |  |
