SINGLE TONE DETECTION | Chapter Thirteen. Digital Signal Processing Tricks

In this section we present an IIR filter structure used to perform spectrum analysis in the detection and measurement of single sinusoidal tones. The standard method for spectral energy is the discrete Fourier transform (DFT), typically implemented using a fast Fourier transform (FFT) algorithm. However, there are applications that require spectrum analysis only over a subset of the N bin-center frequencies of an N-point DFT. A popular, as well as efficient, technique for computing sparse FFT results is the Goertzel algorithm, using an IIR filter implementation to compute a single complex DFT spectral bin value based upon N input time samples. The most common application of this process is to detect the presence of a single continuous-wave sinusoidal tone. With that in mind, let's look briefly at tone detection.

It's certainly possible to use the FFT to detect the presence of a single sinusoidal tone in a time-domain sequence x(n). For example, if we wanted to detect a 30 kHz tone in a time-domain sequence whose sample rate was fs = 128 kHz, we could start by performing a 64-point FFT as shown in Figure 13-41. Then we would examine the magnitude of the X(15) complex sample to see if it exceeds some predefined threshold.

Figure 13-41. DFT method, using an FFT algorithm, to detect a 30 kHz tone.

This FFT method is very inefficient. In our example, we'd be performing 192, (64/2)(log264), complex multiplies to obtain the 64-point complex X(m) in order to compute the one X(15) in which we're interested. We discarded 98% of our computations results! We could be more efficient and calculate our desired X(15) using the single-point discrete Fourier transform (DFT) in Eq. (13-77), which requires N = 64 complex multiplies using

That would be an improvement but, happily, there's a better way. It's called the Goertzel algorithm (pronounced: girt'zel).

13.17.1 Goertzel Algorithm

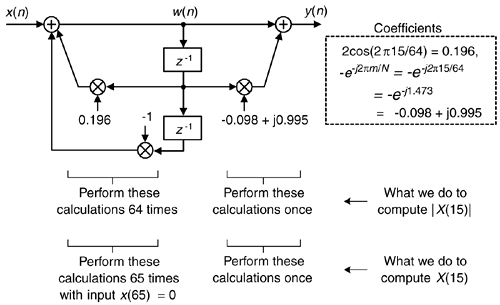
The Goertzel algorithm is implemented in the form of a second-order IIR filter, with two real feedback coefficients and a single complex feedforward coefficient, as shown in Figure 13-42. (Although we don't use this process as a traditional filter, common terminology refers to the structure as a filter.) This filter computes a single-bin DFT output (the mth bin of an N-point DFT) defined by

Equation 13-78

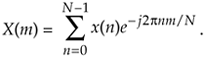
Figure 13-42. IIR filter implementation of the Goertzel algorithm.

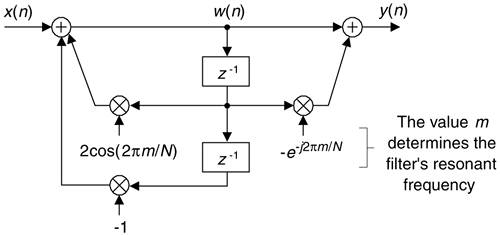
The filter's y(n) output is equal to the DFT output frequency coefficient, X(m), at the time index n = N, where the first time index value is n = 0. For emphasis, we remind the reader that the filter's y(n) output is not equal to X(m) at any time index when n N. To be equivalent to the DFT, the frequency-domain index m must an integer in the range 0 m N–1. You're welcome to think of the Goertzel algorithm as a single-bin DFT. The derivation of this filter (this algorithm) structure is readily available in the literature[44–46].

The z-domain transfer function of the Goertzel filter is

Equation 13-79

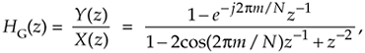
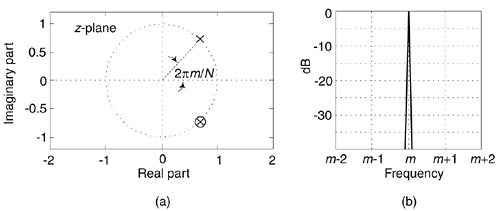
with a single z-domain zero located at z = e–j2pm/N and conjugate poles at z = e±j2pm/N as shown in Figure 13-43(a). The pole/zero pair at z = e–j2pm/N cancel each other. Having a filter pole on the unit circle is typically a risky thing to do for stability reasons, but not so with the Goertzel algorithm. Because it processes N+1-length blocks of time samples (where N is usually in the hundreds), the filter remains stable for such short time sequences because its internal data storage registers, w(n–1) and w(n–2), are reset to zero at the beginning of each new block of input data. The filter's frequency magnitude response, provided in Figure 13-43(b), shows resonance centered at a normalized frequency of 2pm/N, corresponding to a cyclic frequency of mfs/N Hz (where fs is the signal sample rate).

Figure 13-43. Goertzel filter: (a) z-domain pole/zero locations; (b) frequency magnitude response.

The Goertzel algorithm is implemented with a complex resonator having an infinite-length unit impulse response, h(n) = ej2pnm/N, and that's why its frequency magnitude response is so narrow. The time-domain difference equations for the Goertzel filter are

Equation 13-80

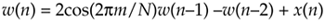
Equation 13-81

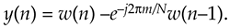
An advantage of the Goertzel filter in computing an N-point X(m) DFT bin value is that Eq. (13-80) is implemented N times while Eq. (13-81), the feed forward path in Figure 13-42, need only be computed once after the arrival of the Nth input sample. Thus for real x(n) inputs the filter requires N+2 real multiplies and 2N+1 real adds to compute an N-point X(m). However, when modeling the Goertzel filter if the time index begins at n = 0, the filter must process N+1 time samples with x(N) = 0 to compute X(m).

In typical applications, to minimize spectral leakage, we choose N so there's an integer number of cycles in our input sequence of the tone we're trying to detect. N can be any integer, and the larger N the better the frequency resolution and noise immunity. However, larger N means more computations.

It's worth noting that while the typical Goertzel algorithm description in the literature specifies the frequency resonance variable m to be an integer (making the Goertzel filter's output equivalent to an N-point DFT bin output), the m in Figure 13-42 and Eq. (13-79) can in fact be any value between 0 and N–1, giving us full flexibility in specifying our filter's resonant frequency.

13.17.2 Goertzel Example

Let's use Goertzel to calculate the spectral magnitude of that ftone = 30 kHz tone from the Figure 13-41 example. When fs = 128 kHz and N = 64, then our resonant frequency integer m is

Equation 13-82

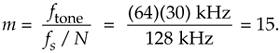
The Goertzel filter and the necessary computations for our 30 kHz detection example are provided in Figure 13-44.

Figure 13-44. Filter, coefficients, and computations to detect the 30 kHz tone.

It's useful to know that if we want to compute the power of X(15), |X(15)2|, the final feedforward complex calculations can be avoided by computing:

Equation 13-83

In our example, Eq. (13-83) becomes

Equation 13-84

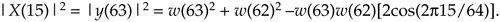
13.17.3 Goertzel Advantages over the FFT

Here are some implementation advantages of the Goertzel algorithm over the standard radix-2 FFT for single tone detection:

N does not need to be an integer power of 2.
The resonant frequency can be any value between zero and fs Hz.
The amount of filter coefficient (versus FFT twiddle factor) storage is reduced. If Eq. (13-83) is used, only one coefficient need be stored.
No storing a block of input data is needed before processing can begin (as with the FFT). Processing can begin with first input time sample.
No data bit reversal is needed for Goertzel.
If you implement the Goertzel algorithm M times to detect M different tones, Goertzel is more efficient (fewer multiplies) than the FFT when M < log2N.
Computational requirements to detect a single tone (assuming real-only x(n) input) are given in Table 13-4.

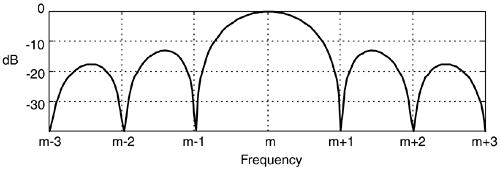
As a final note, although the Goertzel algorithm is implemented with a complex resonating filter structure, it's not used as a typical filter where we retain each output sample. For the Goertzel algorithm we retain only every Nth, or (N+1)th, output sample. As such, the frequency magnitude response of the Goertzel algorithm when treated as a black-box process is equivalent to the |sin(x)/x|-like magnitude response of a single bin of an N-point DFT, a portion of which is shown in Figure 13-45.

Figure 13-45. Goertzel algorithm frequency magnitude response.