THE DFT FREQUENCY RESPONSE TO A REAL COSINE INPUT
Now that we know what the DFT frequency response is to a complex sinusoidal input, it's easy to determine the DFT frequency response to a real input sequence. Say we want the DFT's response to a real cosine sequence, like that shown in Figure 3-40(a), expressed as

where k is the integral number of complete cycles occurring in the N samples. Remembering Euler's relationship cos(ø) = (ejø + e–jø)/2, we can show the desired DFT as Xr(m) where
Equation 3-72
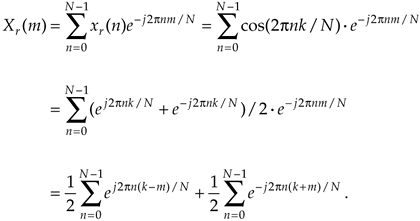
Fortunately, in the previous section we just finished determining the closed form of a summation expression like those in Eq. (3-72), so we can write the closed form for Xr(m) as
Equation 3-73
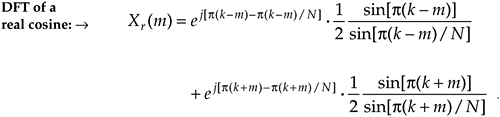
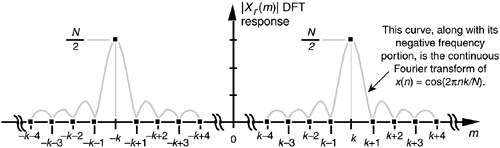
We show the magnitude of those two ratio of sines terms as the sinc functions in Figure 3-43. Here again, the DFT is sampling the input cosine sequence's continuous spectrum and, because k = m, only one DFT bin is nonzero. Because the DFT's input sequence is real, Xr(m) has both positive and negative frequency components. The positive frequency portion of Figure 3-43 corresponds to the first ratio of sines term in Eq. (3-73) and the second ratio of sines term in Eq. (3-73) produces the negative frequency components of Xr(m).
Figure 3-43. N-point DFT frequency magnitude response to a real cosine having integral k cycles in the N-point time sequence xr(n) = cos(2pnk/N).
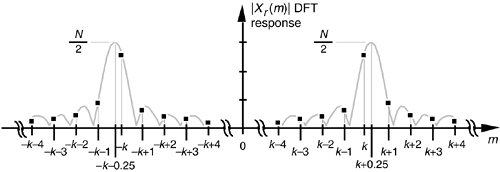
DFT leakage is again demonstrated if our input sequence frequency were shifted from the center of the kth bin to k+0.25 as shown in Figure 3-44. (We used this concept of real input DFT amplitude response to introduce the effects of DFT leakage in Section 3.8.)
Figure 3-44. N-point DFT frequency magnitude response showing spectral leakage of a real cosine having k+0.25 cycles in the N-point time sequence xr(n).
In Table 3-4, the various mathematical expressions for the (positive frequency) amplitude response of the DFT to a real cosine input sequence are simply those expressions in Table 3-3 reduced in amplitude by a factor of 2.
URL http://proquest.safaribooksonline.com/0131089897/ch03lev1sec15
 |
Amazon |  |
