Section E.3. ABSOLUTE POWER USING DECIBELS
E 3 ABSOLUTE POWER USING DECIBELS
Let's discuss another use of decibels that the reader may encounter in the literature. It's convenient for practitioners in the electronic communications field to measure continuous signal-power levels referenced to a specific absolute power level. In this way, they can speak of absolute power levels in watts while taking advantage of the convenience of decibels. The most common absolute power reference level used is the milliwatt. For example, if P2 in Eq. (E-2) is a reference power level of one milliwatt, then
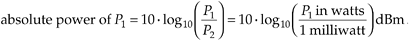
The dBm unit of measure in Eq. (E-10) is read as "dB relative to a milliwatt." Thus, if a continuous signal is specified as having a power of 3 dBm, we know that the signal's absolute power level is 2 times one milliwatt, or 2 milliwatts. Likewise, a –10 dBm signal has an absolute power of 0.1 milliwatts.[ ]
]
[
] Other absolute reference power levels can be used. People involved with high-power transmitters sometimes use a single watt as their reference power level. Their unit of power using decibels is the dBW, read as "dB relative to a watt." In this case, for example, 3 dBW is equal to a 2 watt power level.
The reader should take care not to inadvertently use dB and dBm interchangeably. They mean very different things. Again, dB is a relative power level relationship, and dBm is an absolute power level in milliwatts.
URL http://proquest.safaribooksonline.com/0131089897/app05lev1sec3
 |
Amazon |  |
