TIME-DOMAIN ANALYTIC SIGNAL GENERATION
In digital communications applications, the FIR implementation of the HT (such as that in Figure 9-12(b)) is used to generate a complex analytic signal xc(n). Some practitioners now use a time-domain complex filtering technique to achieve analytic signal generation when dealing with real bandpass signals[8]. This scheme, which does not specifically perform the HT of an input sequence xr(n), uses a complex filter implemented with two real FIR filters with essentially equal magnitude responses, but whose phase responses differ by exactly 90o, as shown in Figure 9-15.
Figure 9-15. Generating an xc(n) sequence with a complex filter (two real FIR filters).
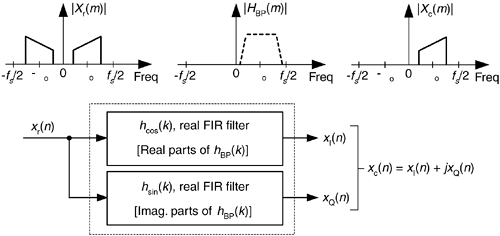
Here's how it's done. A standard K-tap FIR lowpass filter is designed, using your favorite FIR design software, to have a two-sided bandwidth slightly wider than the original real bandpass signal of interest. The real coefficients of the lowpass filter, hLP(k), are then multiplied by the complex exponential 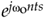 , using the following definitions:
, using the following definitions:
|
wo |
= |
center frequency, in radians/second, of original bandpass signal, (wo = 2pfo) |
|
fo |
= |
center frequency, in Hz |
|
n |
= |
time index of the lowpass filter coefficients (n = 0,1,2,...K–1) |
|
ts |
= |
time between samples, measured in seconds (ts = 1/fs) |
|
fs |
= |
sample rate of the original xr(n) bandpass signal sequence. |
The results of the 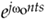 multiplication are complex coefficients whose rectangular-form representation is
multiplication are complex coefficients whose rectangular-form representation is
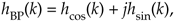
creating a complex bandpass filter centered at fo Hz.
Next we use the real and imaginary parts of the filter's hBP(k) coefficients in two separate real-valued coefficient FIR filters as shown in Figure 9-15. In DSP parlance, the filter producing the xI(n) sequence is called the I-channel for in-phase, and the filter generating xQ(n) is called the Q-channel for quadrature phase. There are several interesting aspects of this mixing analytic signal generation scheme in Figure 9-15:
- The mixing of the hLP(k) coefficients by
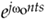 induces a loss, by a factor of 2, in the frequency magnitude responses of the two real FIR filters. Doubling the hLP(k) values before mixing will eliminate the loss.
induces a loss, by a factor of 2, in the frequency magnitude responses of the two real FIR filters. Doubling the hLP(k) values before mixing will eliminate the loss. - We can window the hLP(k) coefficients before mixing to reduce the passband ripple in, and to minimize differences between, the magnitude responses of the two real filters. (We'd like to keep the passband gains as similar as possible.) Of course, windowing will degrade the lowpass filter's rolloff somewhat, so using more coefficients may be necessary before windowing is applied.
- Odd or even-tap lowpass filters can be used, with equal ease, in this technique.
- If either hcos(k) or hsin(k) is symmetrical, the folded FIR structure (see Section 13.7) can be used to reduce the number of multiplies per filter output sample by a factor of two.
- If the original bandpass signal and the complex bandpass filter are centered at one fourth the sample rate (fs/4), count your blessings, because nearly half the coefficients of each real filter are zeros reducing our FIR computational workload further by a factor of two.
- A particularly efficient complex bandpass filter is a half-band FIR filter whose center frequency has been translated to fo = fs/4. In this case half the hcos(k) coefficients are zeros, and all but one of the hsin(k) coefficients are zeros!
- For hardware applications, both of the two real FIR filters in Figure 9-15 must be implemented. If your analytic signal generation is strictly a high-level software language exercise, such as using MATLAB, the language being used may allow hBP(k) to be implemented as a single complex filter.
Keep in mind now, the xQ(n) sequence in Figure 9-15 is not the Hilbert transform of the xr(n) input. That wasn't our goal here. Our intent was to generate an analytic xc(n) sequence whose xQ(n) quadrature component is the Hilbert transform of the xI(n) in-phase sequence.
URL http://proquest.safaribooksonline.com/0131089897/ch09lev1sec5
 |
Amazon |  |
