DECIMATION
Sampling rate changes come in two flavors: rate decreases and rate increases. Decreasing the sampling rate is known as decimation. (The term decimation is somewhat of a misnomer, because decimation originally meant to reduce by a factor of ten. Currently, decimation is the term used for reducing the sample rate by any integer factor.) When the sampling rate is being increased, the process is known as interpolation, i.e., estimating intermediate sample values. Because decimation is the simplest of the two rate changing schemes, let's explore it first.
We can decimate, or downsample, a sequence of sampled values by a factor of D by retaining every Dth sample and discarding the remaining samples. Relative to the original sample rate, fold, the new sample rate is
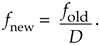
For example, to decimate a sequence xold(n) by a factor of D = 3, we retain xold(0) and discard xold(1) and xold(2), retain xold(3) and discard xold(4) and xold(5), retain xold(6), and so on as shown in Figure 10-1. So xnew(n) = xold(3n), where n = 0, 1, 2, etc. The result of this decimation process is identical to the result of originally sampling at a rate of fnew = fold/3 to obtain xnew(n).
Figure 10-1. Sample rate conversion: (a) original sequence; (b) decimated by three sequence.
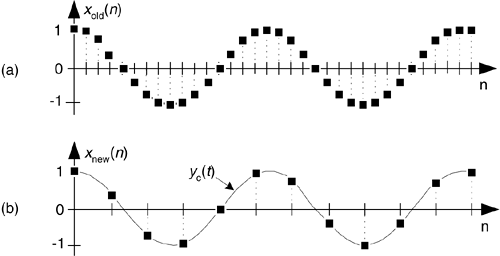
The spectral implications of decimation are what we should expect as shown in Figure 10-2, where the spectrum of an original bandlimited continuous signal is indicated by the solid lines. Figure 10-2(a) shows the discrete replicated spectrum of xold(n), Xold(m). With xnew(n) = xold(3n), the discrete spectrum Xnew(m) is shown in Figure 10-2(b). Two important features are illustrated in Figure 10-2. First, Xnew(m) could have been obtained directly by sampling the original continuous signal at a rate of fnew, as opposed to decimating xold(n) by a factor of 3. And second, there is of course a limit to the amount of decimation that can be performed relative to the bandwidth of the original signal, B. We must ensure fnew > 2B to prevent aliasing after decimation.
Figure 10-2. Decimation by a factor of three: (a) spectrum of original signal; (b) spectrum after decimation by three; (c) bandwidth B' is to be retained; (d) lowpass filter's cutoff frequency relative to bandwidth B'.
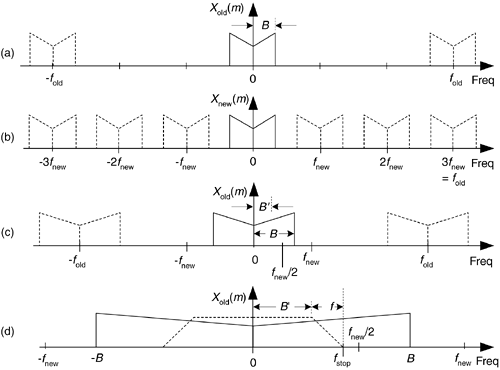
When an application requires fnew to be less than 2B, then xold(n) must be lowpass filtered before the decimation process is performed, as shown in Figure 10-2(c). If the original signal has a bandwidth B, and we're interested in retaining only the band B', the signal above B' must be lowpass filtered, with full attenuation in the stopband beginning at fstop, before the decimation process is performed. Figure 10-2(d) shows this in more detail where the frequency response of the lowpass filter, shaded, must attenuate the signal amplitude above B'. In practice, the nonrecursive FIR filter structure in Figure 5-13 is the prevailing choice for decimation filters due to its linear phase response[1].
When the desired decimation factor D is large, say D > 10, there is an important feature of the filter/decimation process to keep in mind. Significant computational savings may be had by implementing decimation in multiple stages as shown in Figure 10-3(a) The decimation (downsampling) operation  D1 means discard all but every D1th sample. The product of D1 and D2 is our desired decimation factor, that is, D1D2 = D. The problem is, given a desired total decimation factor D, what should be the values of D1 and D2 to minimize the number of taps in lowpass filters LPF1 and LPF2? If D = 100, should D1D2 be (5)(20), (25)(4), or maybe (10)(10)? Thankfully, thoughtful DSP pioneers answered this question for us[1]. For two-stage filtering and decimation, the optimum value for D1 is
D1 means discard all but every D1th sample. The product of D1 and D2 is our desired decimation factor, that is, D1D2 = D. The problem is, given a desired total decimation factor D, what should be the values of D1 and D2 to minimize the number of taps in lowpass filters LPF1 and LPF2? If D = 100, should D1D2 be (5)(20), (25)(4), or maybe (10)(10)? Thankfully, thoughtful DSP pioneers answered this question for us[1]. For two-stage filtering and decimation, the optimum value for D1 is
Equation 10-2
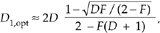
Figure 10-3. Multistage decimation: (a) general decimation block diagram; (b) decimation by 100; (c) spectrum of original signal; (d) output of the D = 25 decimator; (e) output of the D = 4 decimator.
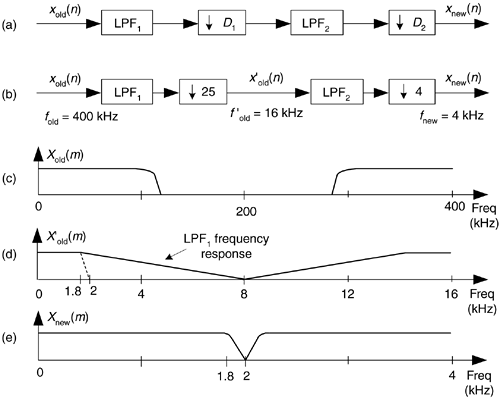
where F is our final transition region width over the stopband frequency, i.e., F = Df/fstop. Upon establishing D1,opt, the second decimation factor is
Equation 10-2'
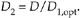
By way of example, let's assume we have input data arriving at a sample rate of 400 kHz, and we must decimate by a factor of D = 100 to obtain a final sample rate of 4 kHz. Also, let's assume the baseband frequency range of interest is from 0 to B' = 1.8 kHz.
So, with fnew = 4 kHz, we must filter out all xold(n) signal energy above fnew/2 by having our filter transition region be between 1.8 kHz and fstop = fnew/2 = 2 kHz. Now let's estimate the number of taps, T, required of a single-stage filter/decimate operation. It's been shown that the number of taps T in a standard tapped-delay line FIR lowpass filter is proportional to the ratio of the original sample rate over the filter transition band, Df in Figure 10-2(d)[1,2]. That is,
Equation 10-3

where 2 < k < 3 depending on the desired filter passband ripple and stopband attenuation. So for our case, if k is 2 for example, T = 2(400/0.2) = 4000. Think of it: a FIR filter with 4000 taps (coefficients)! Next let's partition our decimation problem into two stages: with D = 100 and F = (0.2 kHz/2 kHz), Eq. (10-2) yields an optimum D1,opt decimation factor of 31.9. The closest integer submultiple of 100 to 31.9 is 25, so we set D1 = 25 and D2 = 4 as shown in Figure 10-3(b).
We'll assume the original Xold(m) input signal spectrum extends from zero Hz to something greater than 100 kHz, as shown in Figure 10-3(c). If the first lowpass filter LPF1 has a cutoff frequency of 1.8 kHz and its stopband is defined to begin at 8 kHz, the output of the D = 25 decimator will have the spectrum shown in Figure 10-3(d) where our 1.8 kHz band of interest is shaded. When LPF2 has a cutoff frequency of 1.8 kHz and fstop is set equal to fnew/2 = 2 kHz, the output of the D = 4 decimator will have our desired spectrum shown in Figure 10-3(e). The point is, the total number of taps in the two lowpass filters, Ttotal, is greatly reduced from the 4000 needed by a single filter stage. From Eq. (10-3) for the combined LPF1 and LPF2 filters,
Equation 10-4
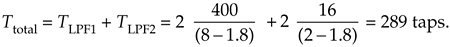
This is an impressive computational savings. Reviewing Eq. (10-3) for each stage, we see in the first stage while fold = 400 kHz remained constant, we increased Df. In the second stage, both Df and fold were reduced. The fact to remember in Eq. (10-3) is the ratio fold/Df has a much more profound effect than k in determining the number of taps necessary in a lowpass filter. This example, although somewhat exaggerated, shows the kind of computational savings afforded by multistage decimation. Isn't it interesting that adding more processing stages to our original D = 100 decimation problem actually decreased the necessary computational requirement?
Just so you'll know, if we'd used D1 = 50 and D2 = 2 (or D1 = 10 and D2 = 10) in our decimation by 100 example, the total number of filter taps would have been well over 400. Thus D1 = 25 and D2 = 4 is the better choice.
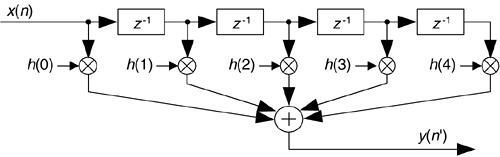
The actual implementation of a filter/decimation process is straightforward. Going back to our original D = 3 decimation example and using the standard tapped-delay line linear-phase FIR filter in Figure 10-4, we compute a y(n') output sample, clock in D = 3 new x(n) samples, and compute the next y(n') output, clock in three new x(n) samples and compute the following y(n') output, and so on. (If our odd-order FIR filter coefficients are symmetrical, such that h(4) = h(0), and h(3) = h(1), there's a clever way to further reduce the number of necessary multiplications, as described in Section 13.7.)
Figure 10-4. Decimation filter implementation.
Before we leave the subject, we mention two unusual aspects of decimation. First, it's interesting that decimation is one of those rare processes that is not time invariant. From the very nature of its operation, we know if we delay the input sequence by one sample, a decimator will generate an entirely different output sequence. For example, if we apply an input sequence x(n) = x(0), x(1), x(2), x(3), x(4), etc., to a decimator and D = 3, the output y(n) will be the sequence x(0), x(3), x(6), etc. Should we delay the input sequence by one sample, our delayed x'(n) input would be x(1), x(2), x(3), x(4), x(5), etc. In this case the decimated output sequence y'(n) would be x(1), x(4), x(7), etc., which is not a delayed version of y(n). Thus a decimator is not time invariant.
Second, decimation does not cause time-domain signal amplitude loss. A sinusoid with a peak-to-peak amplitude of 10 retains this peak-to-peak amplitude after decimation. However, decimation by D does induce a magnitude loss by a factor of D in the frequency domain. Assume the discrete Fourier transform (DFT) of a 300-sample sinusoidal x(n) sequence is |X(m)|. If we decimate x(n) by D = 3 yielding the 100-sample sinusoidal sequence x'(n), the DFT magnitude of x'(n) will be |X'(m)| = |X(m)|/3. This is because DFT magnitudes are proportional to the number of time-domain samples transformed.
To conclude our decimation discussion, a little practical DSP engineering advice is offered here: when we can do so without suffering aliasing errors due to overlapped spectral replications, it's smart to consider decimating our signal sequences whenever possible. Lowering the fs sample rate of your processing
- reduces our computational workload (in computations per second);
- reduces the number of time samples we must process—our computations are completed sooner, allowing us to process wider band signals;
- allows lower cost (lower clock rate) hardware components to be used in hardware-specific implementations;
- yields reduced hardware-power consumption (important for battery-powered devices);
- permits increasing our signal-to-noise ratio by filtering a signal (contaminated with noise) followed by decimation.
With that said, think about decimating your signals whenever it's sensible to do so.
URL http://proquest.safaribooksonline.com/0131089897/ch10lev1sec1
 |
Amazon |  |
