HINTS ON USING FFTS IN PRACTICE
Based on how useful FFTs are, here's a list of practical pointers, or tips, on acquiring input data samples and using the radix-2 FFT to analyze real-world signals or data.
4.2.1 Sample Fast Enough and Long Enough
When digitizing continuous signals with an A/D converter, for example, we know, from Chapter 2, that our sampling rate must be greater than twice the bandwidth of the continuous A/D input signal to prevent frequency-domain aliasing. Depending on the application, practitioners typically sample at 2.5 to four times the signal bandwidth. If we know that the bandwidth of the continuous signal is not too large relative to the maximum sample rate of our A/D converter, it's easy to avoid aliasing. If we don't know the continuous A/D input signal's bandwidth, how do we tell if we're having aliasing problems? Well, we should mistrust any FFT results that have significant spectral components at frequencies near half the sample rate. Ideally, we'd like to work with signals whose spectral amplitudes decrease with increasing frequency. Be very suspicious of aliasing if there are any spectral components whose frequencies appear to depend on the sample rate. If we suspect that aliasing is occurring or that the continuous signal contains broadband noise, we'll have to use an analog low-pass filter prior to A/D conversion. The cutoff frequency of the low-pass filter must, of course, be greater than the frequency band of interest but less than half the sample rate.
Although we know that an N-point radix-2 FFT requires N = 2k input samples, just how many samples must we collect before we perform our FFT? The answer is that the data collection time interval must be long enough to satisfy our desired FFT frequency resolution for the given sample rate fs. The data collection time interval is the reciprocal of the desired FFT frequency resolution, and the longer we sample at a fixed fs sample rate, the finer our frequency resolution will be; that is, the total data collection time interval is N/fs seconds, and our N-point FFT bin-to-bin frequency resolution is fs/N Hz. So, for example, if we need a spectral resolution of 5 Hz, then, fs/N = 5 Hz, and

In this case, if fs is, say, 10 kHz, then N must be at least 2,000, and we'd choose N equal to 2048 because this number is a power of 2.
4.2.2 Manipulating the Time Data Prior to Transformation
When using the radix-2 FFT, if we don't have control over the length of our time-domain data sequence, and that sequence length is not an integral power of two, we have two options. We could discard enough data samples so that the remaining FFT input sequence length is some integral power of two. This scheme is not recommended because ignoring data samples degrades our resultant frequency-domain resolution. (The larger N, the better our frequency resolution, right?) A better approach is to append enough zero-valued samples to the end of the time data sequence to match the number of points of the next largest radix-2 FFT. For example, if we have 1000 time samples to transform, rather than analyzing only 512 of them with a 512-point FFT, we should add 24 trailing zero-valued samples to the original sequence and use a 1024-point FFT. (This zero-padding technique is discussed in more detail in Section 3.11.)
FFTs suffer the same ill effects of spectral leakage that we discussed for the DFT in Section 3.8. We can multiply the time data by a window function to alleviate this leakage problem. Be prepared, though, for the frequency resolution degradation inherent when windows are used. By the way, if appending zeros is necessary to extend a time sequence, we have to make sure that we append the zeros after multiplying the original time data sequence by a window function. Applying a window function to the appended zeros will distort the resultant window and worsen our FFT leakage problems.
Although windowing will reduce leakage problems, it will not eliminate them altogether. Even when windowing is employed, high-level spectral components can obscure nearby low-level spectral components. This is especially evident when the original time data has a nonzero average, i.e., it's riding on a DC bias. When the FFT is performed in this case, a large-amplitude DC spectral component at 0 Hz will overshadow its spectral neighbors. We can eliminate this problem by calculating the average of the time sequence and subtract that average value from each sample in the original sequence. (The averaging and subtraction process must be performed before windowing.) This technique makes the new time sequence's average (mean) value equal to zero and eliminates any high-level, 0-Hz component in the FFT results.
4.2.3 Enhancing FFT Results
If we're using the FFT to detect signal energy in the presence of noise and enough time-domain data is available, we can improve the sensitivity of our processing by averaging multiple FFTs. This technique, discussed in Section 11.3, can be implemented to detect signal energy that's actually below the average noise level; that is, given enough time-domain data, we can detect signal components that have negative signal-to-noise ratios.
If our original time-domain data is real-valued only, we can take advantage of the 2N-Point Real FFT technique in Section 13.5 to speed up our processing; that is, a 2N-point real sequence can be transformed with a single N-point complex radix-2 FFT. Thus we can get the frequency resolution of a 2N-point FFT for just about the computational price of performing a standard N-point FFT. Another FFT speed enhancement is the possible use of the frequency-domain windowing technique discussed in Section 13.3. If we need the FFT of unwindowed time-domain data and, at the same time, we also want the FFT of that same time data with a window function applied, we don't have to perform two separate FFTs. We can perform the FFT of the unwindowed data, and then we can perform frequency-domain windowing to reduce spectral leakage on any, or all, of the FFT bin outputs.
4.2.4 Interpreting FFT Results
The first step in interpreting FFT results is to compute the absolute frequency of the individual FFT bin centers. Like the DFT, the FFT bin spacing is the ratio of the sampling rate (fs) over the number of points in the FFT, or fs/N. With our FFT output designated by X(m), where m = 0, 1, 2, 3, . . ., N–1, the absolute frequency of the mth bin center is mfs/N. If the FFT's input time samples are real, only the X(m) outputs from m = 0 to m = N/2 are independent. So, in this case, we need determine only the absolute FFT bin frequencies for m over the range of 0  m
m  N/2. If the FFT input samples are complex, all N of the FFT outputs are independent, and we should compute the absolute FFT bin frequencies for m over the full range of 0
N/2. If the FFT input samples are complex, all N of the FFT outputs are independent, and we should compute the absolute FFT bin frequencies for m over the full range of 0  m
m  N–1.
N–1.
If necessary, we can determine the true amplitude of time-domain signals from their FFT spectral results. To do so, we have to keep in mind that radix-2 FFT outputs are complex and of the form
Equation 4-4

Also, the FFT output magnitude samples,
Equation 4-5

are all inherently multiplied by the factor N/2, as described in Section 3.4, when the input samples are real. If the FFT input samples are complex, the scaling factor is N. So to determine the correct amplitudes of the time-domain sinusoidal components, we'd have to divide the FFT magnitudes by the appropriate scale factor, N/2 for real inputs and N for complex inputs.
If a window function was used on the original time-domain data, some of the FFT input samples will be attenuated. This reduces the resultant FFT output magnitudes from their true unwindowed values. To calculate the correct amplitudes of various time-domain sinusoidal components, then, we'd have to further divide the FFT magnitudes by the appropriate processing loss factor associated with the window function used. Processing loss factors for the most popular window functions are listed in Reference [3].
Should we want to determine the power spectrum XPS(m) of an FFT result, we'd calculate the magnitude-squared values using
Equation 4-6
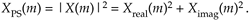
Doing so would allow us to compute the power spectrum in decibels with
Equation 4-7
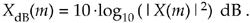
The normalized power spectrum in decibels can be calculated using
Equation 4-8
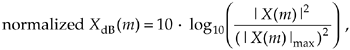
or
Equation 4-9
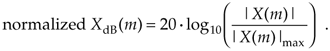
In Eqs. (4-8) and (4-9), the term |X(m)|max is the largest FFT output magnitude sample. In practice, we find that plotting XdB(m) is very informative because of the enhanced low-magnitude resolution afforded by the logarithmic decibel scale, as described in Appendix E. If either Eq. (4-8) or Eq. (4-9) is used, no compensation need be performed for the above-mentioned N or N/2 FFT scale or window processing loss factors. Normalization through division by (|X(m)|max)2 or |X(m)|max eliminates the effect of any absolute FFT or window scale factors.
Knowing that the phase angles Xø(m) of the individual FFT outputs are given by
Equation 4-10
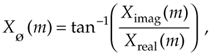
it's important to watch out for Xreal(m) values that are equal to zero. That would invalidate our phase angle calculations in Eq. (4-10) due to division by a zero condition. In practice, we want to make sure that our calculations (or software compiler) detect occurrences of Xreal(m) = 0 and set the corresponding Xø(m) to 90° if Ximag(m) is positive, set Xø(m) to 0° if Ximag(m) is zero, and set Xø(m) to –90° if Ximag(m) is negative. While we're on the subject of FFT output phase angles, be aware that FFT outputs containing significant noise components can cause large fluctuations in the computed Xø(m) phase angles. This means that the Xø(m) samples are only meaningful when the corresponding |X(m)| is well above the average FFT output noise level.
URL http://proquest.safaribooksonline.com/0131089897/ch04lev1sec2
 |
Amazon |  |
