AVERAGING MULTIPLE FAST FOURIER TRANSFORMS
We discussed the processing gain associated with a single DFT in Section 3.12 and stated that we can realize further processing gain by increasing the point size of any given N-point DFT. Let's discuss this issue when the DFT is implemented using the FFT algorithm. The problem is that large FFTs require a lot of number crunching. Because addition is easier and faster to perform than multiplication, we can average the outputs of multiple FFTs to obtain further FFT signal detection sensitivity; that is, it's easier and typically faster to average the outputs of four 128-point FFTs than it is to calculate one 512-point FFT. The increased FFT sensitivity, or noise variance reduction, due to multiple FFT averaging is also called integration gain. So the random noise fluctuations in an FFT's output bins will decrease, while the magnitude of the FFT's signal bin output remains constant when multiple FFT outputs are averaged. (Inherent in this argument is the assumption that the signal is present throughout the observation intervals for all of the FFTs that are being averaged and that the noise sample values are independent of the original sample rate.) There are two types of FFT averaging integration gain: incoherent and coherent.
Incoherent integration, relative to FFTs, is averaging the corresponding bin magnitudes of multiple FFTs; that is, to incoherently average k FFTs, the zeroth bin of the incoherent FFT average Fincoh(0) is given by
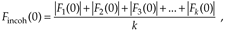
where |Fn(0)| is the magnitude of the zeroth bin from the nth FFT. Likewise, the first bin of the incoherent FFT average, Fincoh(1), is given by
Equation 11-18'
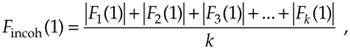
and so on, out to the last bin of the FFT average, Fincoh(N–1), which is
Equation 11-18''
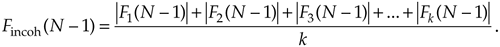
Incoherent integration provides additional reduction in background noise variation to augment a single FFT's inherent processing gain. We can demonstrate this in Figure 11-6(a), where the shaded curve is a single FFT output of random noise added to a tone centered in the 16th bin of a 64-point FFT. The solid curve in Figure 11-6(a) is the incoherent integration of 10 individual 64-point FFT magnitudes. Both curves are normalized to their peak values, so that the vertical scales are referenced to 0 dB. Notice how the variations in the noise power in the solid curve have been reduced by the averaging of the 10 FFTs. The noise power values in the solid curve don't fluctuate as much as the shaded noise-power values. By averaging, we haven't raised the power of the tone in the 16th bin, but we have reduced the peaks of the noise-power values. The larger the number of FFTs averaged, the closer the individual noise-power bin values will approach the true average noise power indicated by the dashed horizontal line in Figure 11-6(a).
Figure 11-6. Single FFT output magnitudes (shaded) and the average of 10 FFT output magnitudes (solid): (a) tone at bin center; (b) tone between bin centers.

When the signal tone is not at a bin center, incoherent integration still reduces fluctuations in the FFT's noise-power bins. The shaded curve in Figure 11-6(b) is a single FFT output of random noise added to a tone whose frequency is halfway between the 16th and 17th bins of the 64-point FFT. Likewise, the solid curve in Figure 11-6(b) is the magnitude average of 10 FFTs. The variations in the noise power in the solid curve have again been reduced by the integration of the 10 FFTs. So incoherent integration gain reduces noise-power fluctuations regardless of the frequency location of any signals of interest. As we would expect, the signal peaks are wider, and the true average noise power is larger in Figure 11-6(b) relative to Figure 11-6(a) because leakage raises the average noise-power level and scalloping loss reduces the FFT bin's output power level in Figure 11-6(b). The thing to remember is that incoherent averaging of FFT output magnitudes reduces the variations in the background noise power but does not reduce the average background noise power. Equivalent to the incoherent averaging results in Section 11.2, the reduction in the output noise variance[6] of the incoherent average of k FFTs relative to the output noise variance of a single FFT is expressed as
Equation 11-19
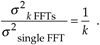
Accordingly, if we average the magnitudes of k separate FFTs, we reduce the noise variance by a factor of k.
In practice, when multiple FFTs are averaged and the FFT inputs are windowed, an overlap in the time-domain sampling process is commonly used. Figure 11-7 illustrates this concept with 5.5Nts seconds worth of time series data samples, and we wish to average ten separate N-point FFTs where ts is the sample period (1/fs). Because the FFTs have a 50 percent overlap in the time domain, some of the input noise in the N time samples for the first FFT will also be contained in the second FFT. The question is "What's the noise variance reduction when some of the noise is common to two FFTs in this averaging scheme?" Well, the answer depends on the window function used on the data before the FFTs are performed. It has been shown that for the most common window functions using an overlap of 50 percent or less, Eq. (11-19) still applies as the level of noise variance reduction[7].
Figure 11-7. Time relationship of multiple FFTs with 50 percent overlap.
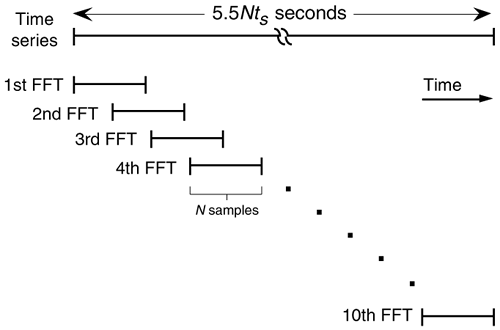
Coherent integration gain is possible when we average the real parts of multiple FFT bin outputs separately from the average of the imaginary parts and then combine the single real average and the single imaginary average into a single complex bin output average value; that is, to coherently average k separate FFTs, the zeroth bin of the complex coherent FFT average, Fcoh(0), is given by
Equation 11-20
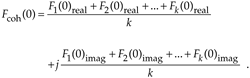
The first bin of the complex coherent FFT average, Fcoh(1), is
Equation 11-20'
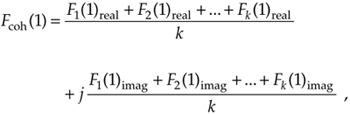
and so on out to the last bin of the complex FFT average, Fcoh(N–1), which is
Equation 11-20''
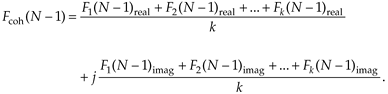
Let's consider why the integration gain afforded by coherent averaging is more useful than the integration gain from incoherent averaging. Where incoherent integration does not reduce the background noise-power average level, it does reduce the variations in the averaged FFT's background noise power because we're dealing with magnitudes only, and all FFT noise bin values are positive—they're magnitudes. So their averaged noise bin magnitude values will never be zero. On the other hand, when we average FFT complex bin outputs, those complex noise bin values can be positive or negative. Those positive and negative values, in the real or imaginary parts of multiple FFT bin outputs, will tend to cancel each other. This means that noise bin averages can approach zero before we take the magnitude, while a signal bin average will approach its true nonzero magnitude. If we say that the coherently averaged FFT signal-to-noise ratio is expressed by
Equation 11-21
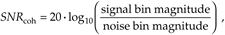
we can see that, should the denominator of Eq. (11-21) approach zero, then SNRcoh can be increased. Let's look at an example of coherent integration gain in Figure 11-8(a), where the shaded curve is a single FFT output of random noise added to a tone centered in the 16th bin of a 64-point FFT. The solid curve in Figure 11-8(a) is the coherent integration of ten 64-point FFTs. Notice how the new noise-power average has actually been reduced.[ ] That's coherent integration. The larger the number of FFTs averaged, the greater the reduction in the new noise-power average.
] That's coherent integration. The larger the number of FFTs averaged, the greater the reduction in the new noise-power average.
[
] The sharp-eyed reader might say, "Wait a minute. Coherent integration seems to reduce the noise-power average, but it doesn't look like it reduces the noise-power variations." Well, the noise-power variations really are reduced in magnitude—remember, we're using a logarithmic scale. The magnitude of a half-division power variation between –20 dB and –30 dB is smaller than the magnitude of a half-division power variation between –10 dB and –20 dB.
Figure 11-8. Single FFT output magnitudes (shaded) and the coherent integration of 10 FFT outputs (solid): (a) tone at bin center; (b) tone between bin centers; (c) tone at bin center with random phase shift induced prior to the FFT process.
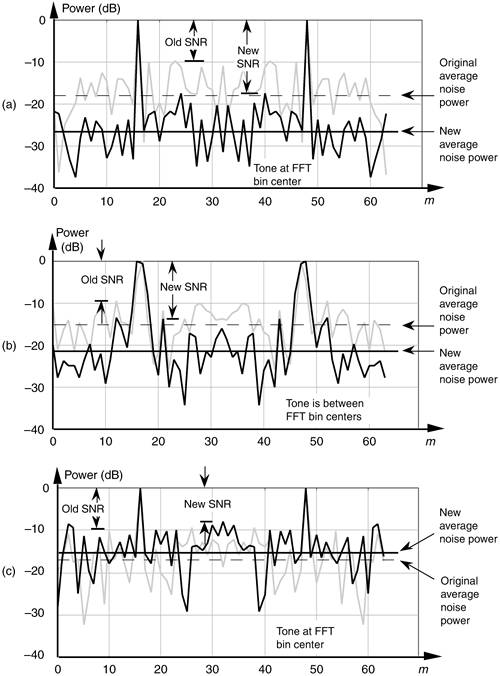
When the signal tone is not at bin center, coherent integration still reduces the new noise-power average, but not as much as when the tone is at bin center. The shaded curve in Figure 11-8(b) is a single FFT output of random noise added to a tone whose frequency is halfway between the 16th and 17th bins of the 64-point FFT. Likewise, the solid curve in Figure 11-8(b) is the coherent integration of 10 FFTs. The new noise-power average has, again, been reduced by the integration of the 10 FFTs. Coherent integration provides its maximum gain when the original sample rate fs is an integral multiple of the tone frequency we're trying to detect. That way the tone will always have the same phase angle at the beginning of the sample interval for each FFT. So, if possible, the fs sample rate should be chosen to ensure that the tone of interest, assuming it's not drifting in frequency, will be exactly at a FFT bin center.
Keep two thoughts in mind while using coherent integration of multiple FFTs. First, if the random noise contaminating the time signal does not have an average value of zero, there will be a nonzero DC term in the averaged FFT's Fcoh(0) bin. Averaging, of course, will not reduce this DC level in the averaged FFT Fcoh(0) output. Second, coherent integration can actually reduce the averaged FFT's SNR if the tone being detected has a random phase at the beginning of each FFT sample interval. An example of this situation is as follows: the shaded curve in Figure 11-8(c) is a single FFT output of random noise added to a tone centered in the 16th bin of a 64-point FFT. The solid curve in Figure 11-8(c) is the coherent integration of 10 individual 64-point FFTs. However, for each of the 10 FFTs, a random phase shift was induced in the fixed-frequency test tone prior to the FFT. Notice how the averaged FFT's new average noise power is larger than the original average noise power for the single FFT. When the tone has a random phase, we've actually lost rather than gained SNR because the input tone was no longer phase coherent with the analysis frequency of the FFT bin.
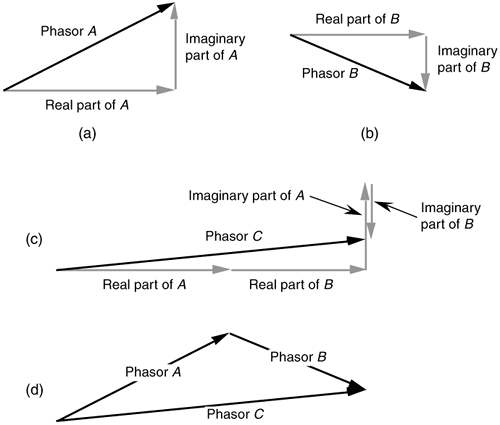
There's a good way to understand why coherent integration behaves the way it does. If we look at the phasors representing the successive outputs of a FFT bin, we can understand the behavior of a single phasor representing the sum of those outputs. But, first, let's refresh our memory for a moment concerning the vector addition of two phasors.[ ] Because an FFT bin output is a complex quantity with a real and an imaginary part, we can depict a single FFT bin output as a phasor, like phasor A shown in Figure 11-9(a). We can depict a subsequent output from the same FFT bin as phasor B in Figure 11-9(b). There are two ways to coherently add the two FFT bin outputs, i.e., add phasors A and B. As shown in Figure 11-9(c), we can add the two real parts and add the two imaginary parts to get the sum phasor C. A graphical method of summing phasors A and B, shown in Figure 11-9(d), is to position the beginning of phasor B at the end of phasor A. Then the sum phasor C is the new phasor from the beginning of phasor A to the end of phasor B. Notice that the two C phasors in Figures 11-9(c) and 11-9(d) are identical. We'll use the graphical phasor summing technique to help us understand coherent integration of FFT bin outputs.
] Because an FFT bin output is a complex quantity with a real and an imaginary part, we can depict a single FFT bin output as a phasor, like phasor A shown in Figure 11-9(a). We can depict a subsequent output from the same FFT bin as phasor B in Figure 11-9(b). There are two ways to coherently add the two FFT bin outputs, i.e., add phasors A and B. As shown in Figure 11-9(c), we can add the two real parts and add the two imaginary parts to get the sum phasor C. A graphical method of summing phasors A and B, shown in Figure 11-9(d), is to position the beginning of phasor B at the end of phasor A. Then the sum phasor C is the new phasor from the beginning of phasor A to the end of phasor B. Notice that the two C phasors in Figures 11-9(c) and 11-9(d) are identical. We'll use the graphical phasor summing technique to help us understand coherent integration of FFT bin outputs.
[
] Following the arguments put forth in Section A.2 of Appendix A, we'll use the term phasor, as opposed to the term vector, to describe a single, complex DFT output value.
Figure 11-9. Two ways to add phasors A and B, where phasor C = A + B.
Now we're ready to look at the phasor outputs of an FFT signal bin to see how a single phasor representing the sum of multiple signal bin phasors behaves. Consider the three phasor combinations in Figure 11-10(a). Each phasor is a separate output of the FFT bin containing the signal tone we're trying to detect with coherent integration. The dark arrows are the phasor components due to the tone, and the small shaded arrows are the phasor components due to random noise in the FFT bin containing the tone. In this case, the original signal sample rate is a multiple of the tone frequency, so that the tone phasor phase angle ø is the same at the beginning of the three FFTs, sample intervals. Thus, the three dark tone phasors have a zero phase angle shift relative to one another. The phase angles of the random noise components are random. If we add the three phasor combinations, as a first step in coherent integration, we get the actual phasor sum shown in Figure 11-10(b). The thick shaded vector in Figure 11-10(b) is the ideal phasor sum that would result had there been no noise components in the original three phasor combinations. Because the noise components are reasonably small, the actual phasor sum is not too different from the ideal phasor sum.
Figure 11-10. FFT bin outputs represented as phasors: (a) three outputs from the same bin when the input tone is at bin center; (b) coherent integration (phasor addition) of the three bin outputs; (c) three outputs from the same bin when input tone has a random phase at the beginning of each FFT; (d) coherent integration of the three bin outputs when input tone has random phase.
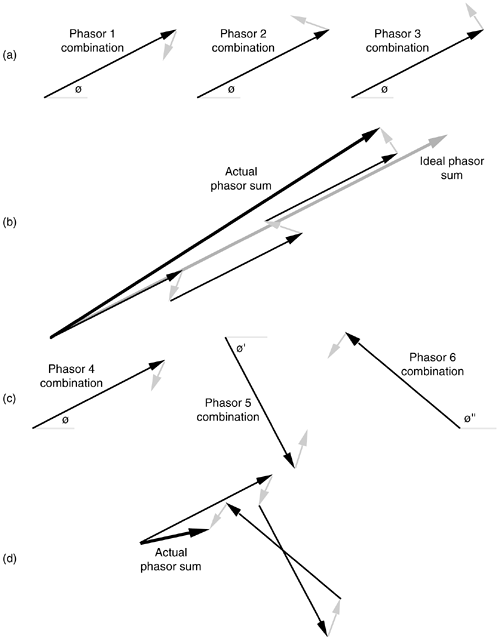
Now, had the original signal samples been such that the input tone's phase angles were random at the beginning of the three FFTs, sample intervals, the three phasor combinations in Figure 11-10(c) could result. Summing those three phasor combinations results in the actual phasor sum shown in Figure 11-10(d). Notice that the random tone phases, in Figure 11-10(c), have resulted in an actual phasor sum magnitude (length) that's shorter than the dark lines of the phasor component due to the tone in Figure 11-10(c). What we've done here is degrade, rather than improve, the averaged FFT's output SNR when the tone has a random phase at the beginning of each FFT sample interval.
The thought to remember is that, although coherent averaging of FFT outputs is the preferred technique for realizing integration gain, we're rarely lucky enough to work real-world signals with a constant phase at the beginning of every time-domain sample interval. So, in practice, we're usually better off using incoherent averaging. Of course, with either integration technique, the price we pay for improved FFT sensitivity is additional computational complexity and slower system response times because of the additional summation calculations.
URL http://proquest.safaribooksonline.com/0131089897/ch11lev1sec3
 |
Amazon |  |
