Key Exchange

So far I've talked about all different kinds of keys: symmetric and asymmetric keys, and encryption and HMAC keys. As I mentioned in the last two sections on encryption and packet authentication, which typically use symmetrical keys, the sharing of the protection keys is a security issue. This next section will explore the key-sharing process in more depth and talk about some possible solutions, such as the following:

• Key Sharing Dilemma
• Diffie-Hellman
• Key Refreshing
• Limitations of Key Exchange Methods

Key Sharing Dilemma

A simple example illustrates the issues of sharing keys for symmetric keying algorithms and functions. You have decided to protect financial data between two devices, PeerA and PeerB, and want to encrypt this information using a special symmetric encryption algorithm. PeerA has decided that the encryption key should be "If you can guess this key, you win a lollipop!" Now the issue is to get this key to PeerB so that it can decrypt your financial data successfully. I'll discuss some possible solutions in the following subsections.

Pre-Share the Key

One solution might be to take the key on PeerA and share it, out-of-band, with PeerB. For instance, you could copy the key to a floppy disk or write it down on a piece of paper and then mail this to PeerB. Or you could just call up PeerB and tell him what the key is over the phone. Both of these are referred to "out-of-band" sharing, since the actual key is not shared across the data network.

One downside to pre-sharing keys is that it doesn't scale very well. For example, if you had 100 peers you needed to share keys with, it would take quite a while to perform this process. At a minimum, you would want to change keys every time an employee left the company who knew the pre-shared keys. Also, you would want to change the keys periodically to make your encryption process more secure, just in the off chance your encryption key was compromised. If your security policy stated that you needed to change the encryption key every hour, this solution would not be feasible because of the out-of-band delay involved in getting the keys between the two peers.

Use an Already Encrypted Connection

If you would attempt to share the encryption key in-band with PeerB, like using Telnet to access PeerB, the key would be susceptible to an eavesdropping attack. One solution is to use an already encrypted connection. You could use a secure program to do this, such as SSH; however, SSH requires keys that would have to be exchanged in a secure fashiona catch-22 situation, because you would need a secure connection to share the SSH keys in the first place.

Encrypt the Key with an Asymmetric Keying Algorithm

I've already (indirectly) discussed one way to solve the symmetric key-sharing issue: use asymmetric encryption. If you recall from the "Asymmetric keys" section, asymmetric keying uses two keys: a public and private key. These keys have a symbiotic relationship with each other and a special algorithm is used to generate these keys. When used for encryption purposes, each peer would generate a public/private key pair. Then each peer would share their public keys with each other. When PeerA would want to send traffic to PeerB, PeerA would use PeerB's public key to encrypt data and then send it to PeerB. PeerB would then use its own private key to decrypt the data.

In our example of financial data, I'll assume that each transfer is 100 MB in size, and this happens every 15 or 20 minutes. This is a large amount of data; asymmetric encryption algorithms are very slow and process-intensive; so they are not desirable when large amounts of data need to be transferred.

However, instead of using asymmetric keying to encrypt the actual financial data, we could, instead, use asymmetric keying to encrypt the symmetric key. This allows us to share the symmetric key across an insecure connection, while sending it in an encrypted format.

In the example of the financial data, PeerA has the encryption key; therefore, PeerB creates a public/private key combination and sends its public key to PeerA. PeerA then takes the symmetric key and encrypts it with PeerB's public key. PeerA sends the encrypted symmetric key, "If you can guess this key, you win a lollipop!", to PeerB, which decrypts it with its own private key. Therefore, whenever PeerB receives encrypted financial data from PeerA, it will be able to decrypt the data successfully with the shared symmetric key. The advantage of this approach is that the asymmetric key encryption process occurs only on the symmetric key: the financial data is encrypted using a symmetric encryption algorithm and the shared symmetric key.

Most VPN implementations use a public/private key algorithm in this way to share symmetric keys. In the next section I'll discuss a public/private key implementation that is commonly used by most VPN implementations today.

Diffie-Hellman Algorithm

The public/private key cryptography process was originally credited to Whitfield Diffie, Martin Hellman, and Ralph Merkle in 1976. Their ideas are covered by U.S. patent 4,200,770, which expired in 1994. The process is commonly referred to as Diffie-Hellman (DH).

However, there is evidence to prove that these three actually didn't discover the public/private key cryptography process; rather it was one of two government agencies of the British or the U.S. (National Security Agency) government 10 years before Diffie, Hellman, and Merkle developed a similar process independently. These processes, however, were kept secret from the public; and whereas this information was classified and never published, these three people created the same solution for public use.

Today our concern is not who discovered the process, but how to share symmetric keys in an insecure network. Most networking vendors look at the Public Key Cryptography Standard (PKCS) #3 standard to implement DH.

Simply put, DH is typically not used to encrypt user data, but is, in most cases, used by VPN implementations to share keying information securely, such as DES, 3DES, AES, SHA, MD5 and other symmetric keys, across an insecure public network, like the Internet. DH uses public key cryptography (asymmetric keying) to accomplish this. Therefore, it is commonly referred to as a public key exchange method.

Many VPN implementations, such as IPsec, use DH to share symmetric encryption keys in a secure fashion. For instance, IPsec's RFCs 2401, 2408, and 2412 rely on the use of DH for sharing of keying information for HMAC functions, such as MD5 and SHA, and encryption algorithms, like DES, 3DES, and AES.

Figure 2-4 explains how DH works. DH uses the following six steps to share symmetric keys across an insecure network:

1.	Each of the two peers shares information that will help them create their own public/private key combinations; this is necessary because DH supports varying key sizes, called key groups. I'll discuss DH key groups after these numbered steps. Once the key size is known, the two peers create their personal public/private key pair combination. Actually, each creates its private key first, and uses a derivative process to derive the public key from the private key.
2.	Each peer shares its public key with the remote peer.
3.	Each peer takes its personal private key and the remote peer's public key and runs them through the DH algorithm.
4.	The mathematical beauty of the DH algorithm is that even though different inputs are fed into the algorithm, the same output results on both sides: Diffie, Hellman, and Merkle figured out that if you have one pair of values that have a relation, and another pair of values that have a relation, when you exchange one value for another in the different pair, there is still a relationship between the values. I have a degree in mathematics, but coming up with this proof is way beyond my abilitiesI'm just glad these three guys made it easier for me to set up secure networks!
5.	Because PeerA created the symmetric encryption key for the financial data, PeerA encrypts the data with the output key from the DH algorithm, Secret_key_X, and sends the encrypted symmetric encryption key to PeerB across the network.
6.	When PeerB receives the encrypted key, PeerB uses the same derived DH key, Secret_key_X, to decrypt the symmetric key, resulting in "If you can guess this key, you win a lollipop!"; therefore, when PeerA sends financial data to PeerB, PeerB will be able to decrypt it successfully with the symmetric encryption key.

Figure 2-4. The Diffie-Hellman Process

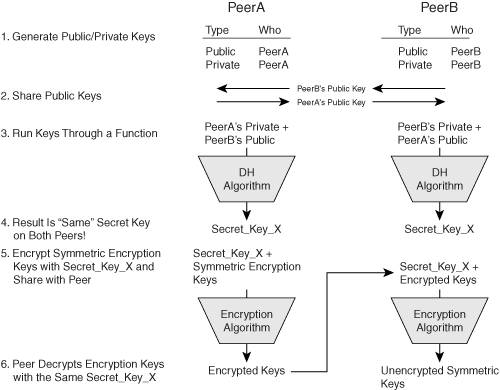
DH uses key groups to define how the shared secret key is actually generated. The key groups define the key length for the public and private keys and the DH algorithm to use in generating the shared secret key.

Table 2-1 has a quick breakdown of the DH key groups. In this table, the first column indicates the name of the key group, denoted by a number. Following this is the length of the keys, and, in the last column, the type of algorithm used to create the shared secret key. DH key groups are commonly referred to with their number, as in DH group 1.

Table 2-1. DH Key Groups

Key Group	Length	Equation
1	768 bits	Straight algorithm
2	1,024 bits	Straight algorithm
3	155 bits	Elliptical curve algorithm
4	185 bits	Elliptical curve algorithm
5	1,536 bits	Straight algorithm (most secure key group supported by Cisco)
7	163 bits	Elliptical curve algorithm
14	2,048 bits	Straight algorithm
15	3,072 bits	Straight algorithm (most secure key group, but Cisco doesn't support it)

Straight algorithms use a normal computation process, like an equation, to produce a secure key. The longer the bit length is for a straight algorithm, the stronger the resulting secret key. But straight algorithms and keys with long bit lengths are very computational-intensive. For example, a Cisco 7200 router with a VAM card would have no problem processing a straight algorithm using DH group 15; however, a personal digital assistant (PDA) device doesn't have that capacity.

To accommodate devices that have limited processing power, elliptical curve algorithms are used; they can use a smaller key size, but can create a more secure result than a corresponding straight algorithm using the same key size. But because they are also process-intensive, the key sizes are kept small so that limited processing devices can still use them.

Note

Remember that if a VPN implementation uses DH, it won't necessarily support all DH groups. For instance, if a Cisco router is using IPsec, it supports only DH groups 1, 2, and 5 (as of the writing of this book); whereas the Cisco VPN 3000 series concentrators support DH groups 1, 2, 5, and 7 for IPsec. Whatever DH groups a device supports for a VPN implementation, in other words, is device- or vendor-specific.

 

Key Refreshing

Another thing to consider is the management of keys. Periodically, you'll probably want to change your symmetric keys used by encryption algorithms and HMAC functions for a more secure solution. For example, if you had 100 sets of keys, and your security policy stated that you should change the keys once every hour, you definitely would not want to do this manuallythis would require multiple full-time people to perform this task 24 hours a day, seven days a week!

Therefore, one of the important features a VPN implementation should support is management of keys: the ability to refresh them periodically in a dynamic, secure, in-band fashion, reducing the amount of physical management to a very small amount of time. For example, DH doesn't specify how to deal with key management functions; however, VPN implementations, such as IPsec, have other components that handle this process.

Limitations of Key Exchange Methods

One strength of asymmetric keying algorithms is that the private key, used to decrypt information, is never sent across the network. And with DH, the derived secret key also never traverses the network. Thus an attacker, even if he is eavesdropping on the public key exchange process and sees the exchanged public key or keys, wouldn't be able to use this to decrypt any transmitted information. In a simple asymmetric algorithm implementation, the eavesdropping attacker would have to know the private key to decrypt information; and in the case of DH, the attacker would have to know of one of the two private keys to decrypt information.

However, DH does have one main weakness: it is susceptible to a man-in-the-middle attack. I'll use the PeerA-to-PeerB example. PeerA needs to encrypt financial data to PeerB. In this example, assume DH is being used for sharing keys. PeerA initiates a connection to PeerB; assume that instead of the real PeerB responding back, a man-in-the-middle attack occurs and the attacker's device responds back. DH, however, assumes that the two devices trust each other. In the PeerA-to-PeerB example, especially if they're separated by a public network, they have no idea if they're interacting with each other, or with some device pretending to be one of the two parties.

In other words, key exchange protocols such as DH deal strictly with one thing: key exchanges. They don't deal with authentication mechanisms. Some other component is required to verify the identities of the two devices to ensure that PeerA doesn't mistakenly send sensitive financial data to a man-in-the-middle device (attacker).