Hack 30. Plot a Great Circle on a Flat Map

Wherein our heroes discover that the shortest distance between two points on a globe is not a straight line, after all.

What's so great about a great circle? A great circle, technically speaking, is any circle that goes all the way around a sphere, with its center on the exact center point of the sphere. As it turns out, when a great circle connects two points on a sphere, the arc between them is always the shortest distance between those two points. Naturally, being able to take the shortest possible path is a matter of great financial and practical importance in this modern era of air travel.

Familiar two-dimensional map projections don't give a good impression of great-circle distance. On a Mercator map, the straight line that seems to be the shortest route between San Francisco and London passes through Boston; but, in fact, due to the curvature of the globe, the actual shortest route runs nearer to the North Pole, passing over the south of Greenland.

This hack makes use of Generic Mapping Tools, or GMT [Hack #28] to show how to plot segments of a great circle on many different cartographic projections, including those designed for marine and aerial navigation. We'll also show you how you can try this yourself with a quick Perl script.

3.10.1. Great Circles on a Mercator Projection

The Mercator projection was historically useful because it preserved navigational direction along lines of constant bearing, known as rhumb lines. One could draw a straight line to one's destination on the map, set off in the direction indicated by that line, and actually arrive at the intended destination sometime in the future. Navigating by a Mercator map therefore had the great advantage of simplicity, but the disadvantage was that the rhumb line between two points was often not the shortest path.

Instead, the shortest path between two points follows a line of variable bearing, which turns out to be the arc of a great circle. This may seem counterintuitive, because a great-circle arc will usually end up looking curved on a flat map. Figure 3-31 depicts the great-circle arc connecting San Francisco and London on a Mercator projection of the world.

Figure 3-31. Great-circle arc from SF to London on a Mercator projection

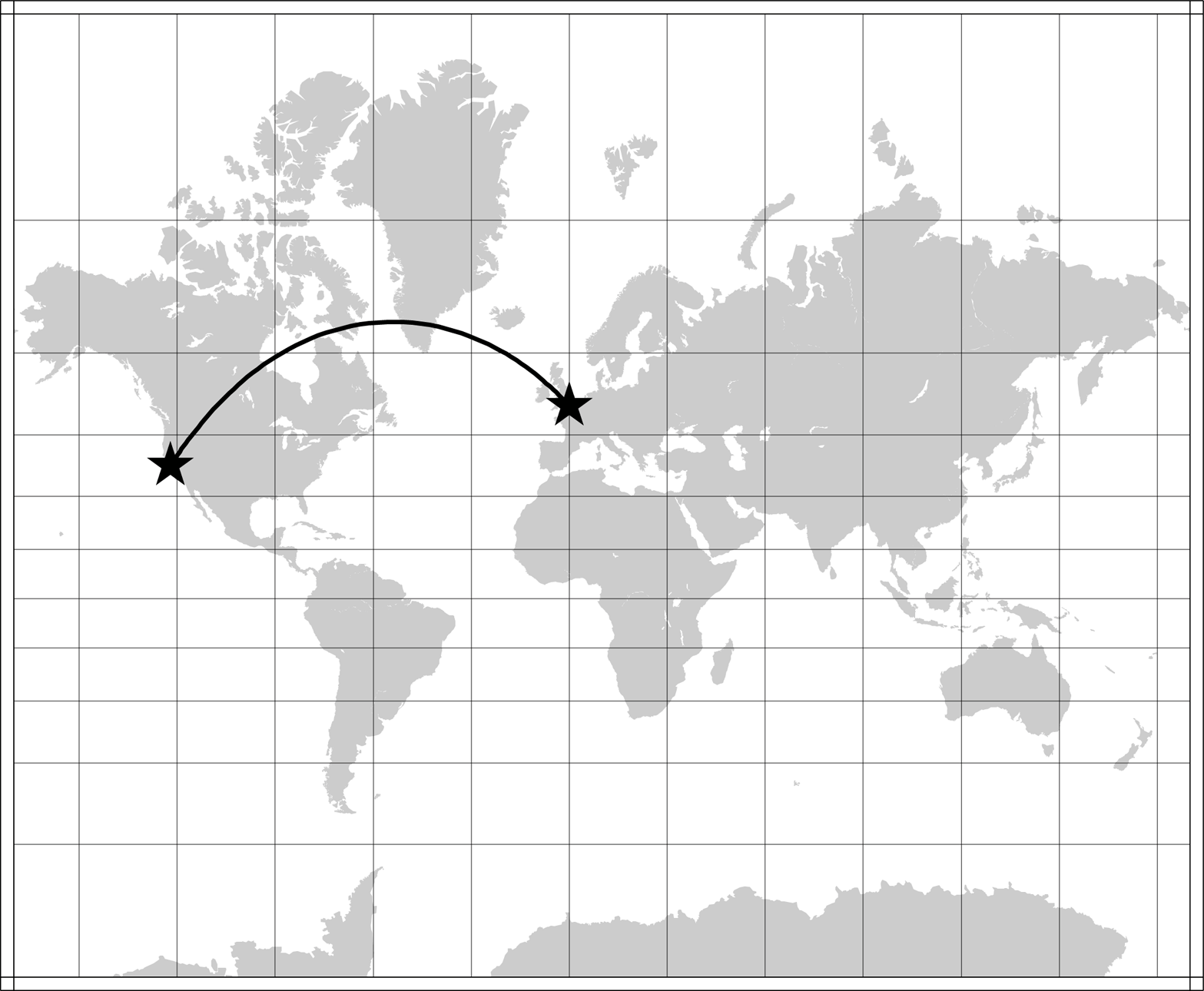
The following commands, using pscoast and psxy from GMT, were used to generate Figure 3-31:

$ pscoast -JM18c -R-170/190/-75/85 -Bg30/g15 -A5000 -G192/192/192 -K >  
mercator.ps
$ psxy points.txt -JM18c -R-170/190/-75/85 -W8 -O -K >> mercator.ps
$ psxy points.txt -JM18c -R-170/190/-75/85 -Sa.75c -G0/0/0 -O >> mercator.ps

The call to pscoast draws the graticule (i.e., grid lines) and the base map of the continents. We recommend reviewing [Hack #28] to understand exactly how these particular pscoast options do their magic. The first call to psxy actually draws the great-circle arc into the same file. We give psxy the same projection parameters we did pscoast, along with a filename, points.txt. The points.txt file simply contains the following:

-122,38
0,51

The geographically savvy reader will recognize these as the longitude and latitude coordinates of San Francisco and London, respectively. The -W8 option to psxy tells it to make the great-circle arc 8 pixels thick. Finally, we call psxy one more time, with the same projection parameters and filename containing our points, but this time we give the -S option to request that symbols be drawn at each point, instead of a line connecting them. In this case, the -Sa.75c option draws us a star .75 centimeters wide at each end point, coloring each one black via the -G option.

The shortest line between two points on any geometric figure is referred to as a geodesic, of which the great circle along a spherical surface is but an example. For this reason, the GRASS command for drawing great circles is called r.geodesic. The word geodesic, which comes from the Greek words for "dividing the Earth," is also used to describe Buckminster Fuller's dome structures, in the way that they systematically divide the surface of a sphere (or hemisphere) into triangular faces.

 

3.10.2. Great Circles on an Orthographic Projection

The fact that a great circle forms the shortest line between two points doesn't seem quite as odd, however, when you look at a globe. Figure 3-32 depicts the same great-circle arc connecting San Francisco and London on an orthographic projection, which presents a flat perspective view of a globe. From this vantage, it becomes evident that the shortest route from San Francisco to London really does sort of run over the curve of the earth, as it were, rather than around it. Consequently, the line that runs between them through Bostonthe line one might have thought was the shortest, looking at a Mercator mapis actually quite hopelessly roundabout.

Figure 3-32. Great-circle arc from San Francisco to London on an orthographic projection

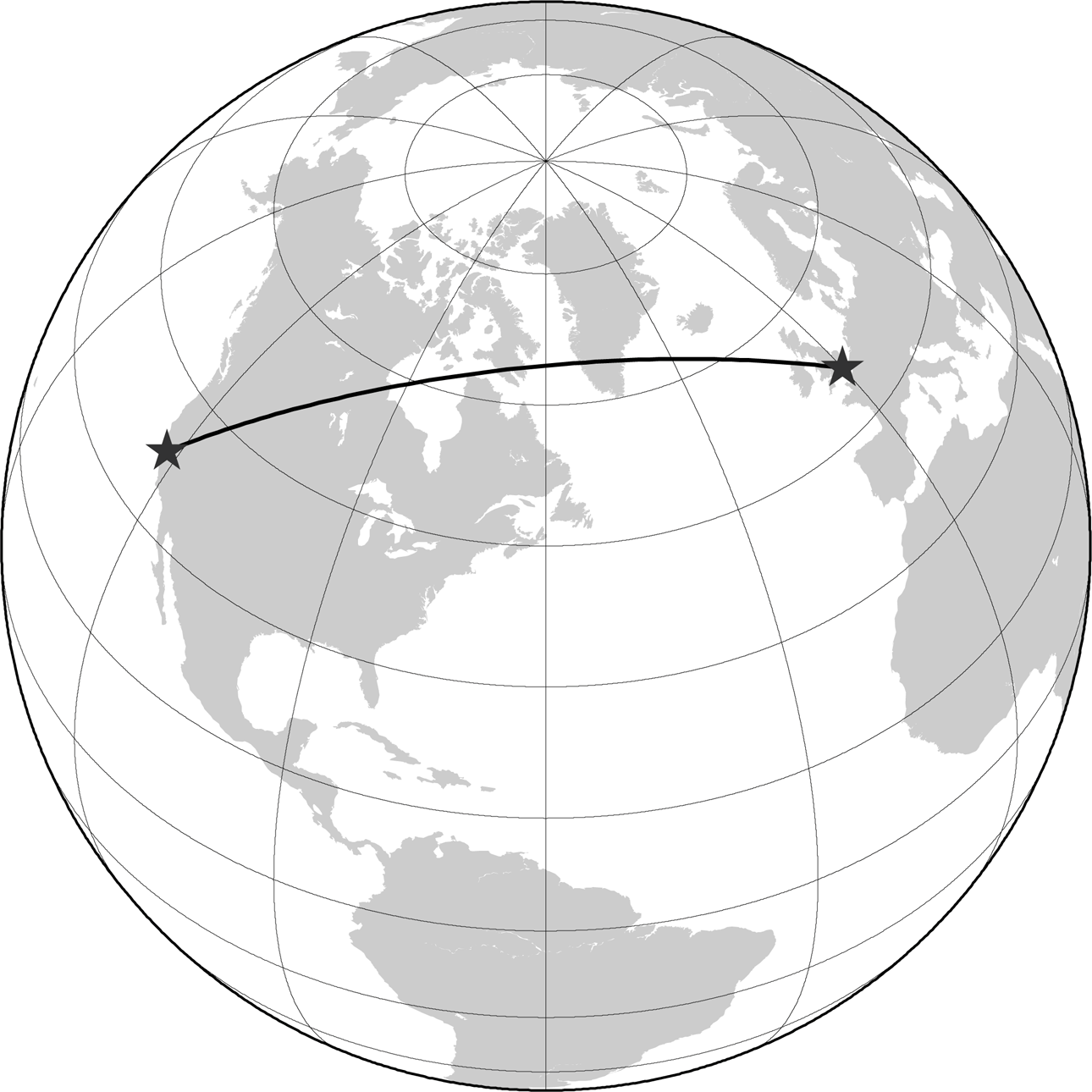
Figure 3-32 was made using the same GMT commands as Figure 3-31, except that the -JM18c parameter for generating a Mercator projection was replaced with -JG-60/45/18c, which draws an orthographic projection 18 centimeters wide, centered on 60º W and 45º N.

3.10.3. Great Circles on a Gnomonic Projection

There are other ways to visualize great circles on a flat map, of course. If we want a map that depicts the shortest distance between two points as a straight line, we can turn to the Gnomonic projection. Basically, any straight line on a Gnomonic projection, regardless of origin or bearing, represents a great-circle arc on Earth's surface. Although the Gnomonic projection distorts the shape and area of landmasses something fierce, the property of showing any great-circle arc as a straight line makes it quite useful for the purposes of air navigation. Figure 3-33 shows the great circle connecting London and San Francisco on a Gnomonic projection of the world. Figure 3-33 was generated with GMT in the same fashion as Figures 3-31 and 3-32, using the -JF-75/60/60/18c option to plot the Gnomonic projection centered on 75º W and 60º N, with a radius of 60º.

Figure 3-33. Great-circle arc from San Francisco to London on a Gnomonic projection

 

3.10.4. Great Circles of Perl

In practice, great-circle routes are hard to navigate precisely, because the bearing of a great circle relative to True North changes continually, unlike that of a rhumb line. In fact, the conventional way to navigate a great-circle route is to approximate it with a series of short rhumb lines. We can use this same technique to draw the path of a great-circle arc on a flat map in Perl:

#!/usr/bin/perl
 
use Math::Trig qw(great_circle_direction deg2rad);
use Imager;
use strict;
 
my ($mapfile, $lon1, $lat1, $lon2, $lat2) = @ARGV;
my @origin = ($lon1, $lat1);
my @dest = ($lon2, $lat2);
my $step = .1;
 
my @position = @origin;
my @points;
 
until (abs($position[0] - $dest[0]) < $step
 and abs($position[1] - $dest[1]) < $step) {
 my $bearing = great_circle_direction(
 deg2rad( $position[0] ),
 deg2rad( 90 - $position[1] ),
 deg2rad( $dest[0] ),
 deg2rad( 90 - $dest[1] )
 );
 
 $position[0] += sin($bearing) * $step / cos(deg2rad($position[1])) ;
 $position[1] += cos($bearing) * $step;
 
 $position[0] += 360 if $position[0] < -180;
 $position[0] -= 360 if $position[0] > 180;
 
 push @points, @position;
}

In the first part of our script, we do the actual approximation of rhumb lines to a great circle, using the great_circle_direction() function from the Math::Trig module, which ships with Perl. We get the name of an image containing an Equidistant Cylindrical projection, as well as the longitude and latitude of our start and end points from the command line. We set @origin to the longitude and latitude of our starting point, and @dest to that of our destination. $step is chosen to roughly approximate the length of each component rhumb line. The current position is stored in @position, which gets initialized to our origin.

At each step, we call great_circle_direction() to find the bearing from True North at our current position along the great circle to our destination. Since great_circle_direction() expects its arguments in radians, not degrees, and places the zero latitude at the North Pole, rather than the equator, we have to make the proper adjustments before passing those values. We store the result in radians in $bearing, which we then use to update our current position.

Updating the latitude of our current position, as stored in $position[1], is easy: simply add the cosine of our bearing scaled by the length of our rhumb line to find the latitude of our next end point. If you dig deep into the mists of your high school trigonometry education, you'll remember why this is so: If we take $step to be the length of the hypotenuse of a right triangle, then the cosine of the bearing is equal to the length of the adjacent side divided by the length of the hypotenuse.

Multiplying both sides of the equation by $step yields the code shown earlier for updating $position[1].

Updating the longitude, however is a little trickier. We could simply take our current longitude, stored in $position[0], and add the sine of our current bearing, scaled by the length of our rhumb line, but we would be ignoring an important fact about our round world. As you head toward the poles, the distance between two lines of longitude gets shorter in proportion to the cosine of the latitude. At the equator, the distance separating one degree of longitude is cos(0º) = 1 degree of latitude. At the North Pole, the distance is cos(90º), which is zero. Thus we divide our longitude increment by the cosine of the current latitude, in order to keep in step with the actual great- circle arc.

Actually, we fibbed slightly. The distance separating one degree of longitude at the equator isn't quite equal to one degree of latitude, because Earth isn't a perfect sphere it's an oblate spheroid, which means it's slightly flattened at the poles and slightly bulged around the middle, due to rotational and tidal forces. Because the difference is insignificant for our purposes, though, we'll otherwise ignore this fact in our discussion.

Finally, we do some bounds checking, to keep our longitude from running off the edge of the map. Having done so, we add our new current position to @points, and repeat, until we're close enough to our destination that it's not worth continuing.

Now that we have a list of longitude/latitude coordinates in @points, representing the end points of the rhumb line segments that approximate our great-circle arc, we can use any suitable method to plot them on a flat map. For simplicity's sake, we'll use the method outlined in [Hack #29] to draw the great-circle arc between San Francisco and London on an Equidistant Cylindrical map of the world. The remainder of our script, then, reads as follows:

my ($top, $left) = ( 90, -180 );
my ($bottom, $right) = ( -90, 180 );
 
my $map = Imager->new;
$map->open( file => $mapfile ) or die $map->errstr;
 
my $x_scale = $map->getwidth / ($right - $left);
my $y_scale = $map->getheight / ($bottom - $top);
 
while (@points) {
 my (@x, @y);
 while (my ($lon, $lat) = splice @points, 0, 2) {
 push @x, ($lon - $left) * $x_scale;
 push @y, ($lat - $top) * $y_scale;
 last if @points and $lon < -170 and $points[0] > -170;
 }
 $map->polyline( x => @x, y => @y, color => "red" );
}
 
$map->write( fh => *STDOUT, type => "jpeg" ) or die $map->
errstr;

Since this method of plotting points on a rectangular map [Hack #29] is explained elsewhere, we'll gloss over the details here. We load the map image stored earlier in $mapfile into an object stored in $map. The crucial bit happens in the while() loop, where we shift coordinate pairs off of @points, and convert the longitude and latitude to x- and y-coordinates on the map image. Once we've done this, we send our lists of x and y end points to $map->polyline(), to draw the actual arc on the map. We have to be sure to test for the case where the arc crosses the international date line, and break the polyline into two parts, if necessary. The last if @points... statement tests for this possibility. Finally, the map is dumped to standard output. The code to run is as follows:

$ perl greatcircle.pl PathfinderMap.jpg -122 38 0 51 > sf_to_london.jpg

We give the script the name of our Equidistant Cylindrical map file [Hack #29] for good sources of such maps), as well as the longitude and latitude of San Francisco and London, in that order. The map, which is shown in Figure 3-34, shows the great-circle arc connecting them. Adding embellishments, such as a marker at each end, is left as an exercise for the reader.

Figure 3-34. Great-circle arc from SF to London, plotted with Perl, on a Equidistant Cylindrical projection

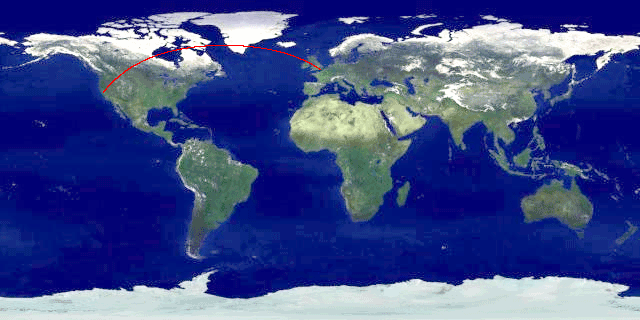
Of course, having found the shortest route from San Francisco to London, you will probably immediately want to know how long that route is, which is a question tackled in [Hack #27] .

3.10.5. See Also

• [Hack #28]
• [Hack #29]
• [Hack #27]